
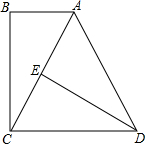
 如图,已知AB∥CD,BC⊥AB,∠CAD=60°,且AD=DC,E是AC的中点,求证:BC=ED.
如图,已知AB∥CD,BC⊥AB,∠CAD=60°,且AD=DC,E是AC的中点,求证:BC=ED. 分析 根据等边三角形的判定与性质得出DE⊥AC,∠BAC=∠ACD=60°,进而求出△ADE≌△ACB(AAS),求出即可.
解答  证明:∵∠CAD=60°且AD=DC,
证明:∵∠CAD=60°且AD=DC,
∴△ACD是等边三角形,
∴AC=AD=CD,∠ACD=60°,
∵E是AC的中点,
∴DE⊥AC,
∵AB∥CD,
∴∠BAC=∠ACD=60°,
∴在△ADE和△ACB中
$\left\{\begin{array}{l}{∠DEA=∠CBA}\\{∠EAD=∠BAC}\\{AD=AC}\end{array}\right.$,
∴△ADE≌△ACB(AAS),
∴BC=ED.
点评 此题主要考查了全等三角形的判定与性质以及等边三角形的判定与性质,得出△ADE≌△ACB是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
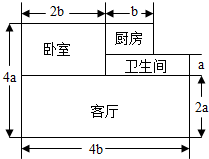 李叔叔买了一套新房,其结构如图(单位:m),他打算除卧室外,其余部分铺地砖.
李叔叔买了一套新房,其结构如图(单位:m),他打算除卧室外,其余部分铺地砖.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 说假话的是甲,作案的是乙 | B. | 说假话的是丁,作案的是丙和丁 | ||
| C. | 假话的是乙,作案的是丙 | D. | 说假话的是丙,作案的是丙 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com