
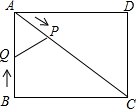
 ��ͼ���ھ���ABCD�У�AB=3��BC=4������P�ӵ�A������AC���յ�C�˶���ͬʱ����Q�ӵ�B������BA���A�˶�������A���������ԭ�����ٶ���AB���أ���P��Q�˶��ٶȾ�Ϊÿ��1����λ���ȣ�����P�����Cʱֹͣ�˶�����QҲͬʱֹͣ������PQ�����˶�ʱ��Ϊt��t��0���룮
��ͼ���ھ���ABCD�У�AB=3��BC=4������P�ӵ�A������AC���յ�C�˶���ͬʱ����Q�ӵ�B������BA���A�˶�������A���������ԭ�����ٶ���AB���أ���P��Q�˶��ٶȾ�Ϊÿ��1����λ���ȣ�����P�����Cʱֹͣ�˶�����QҲͬʱֹͣ������PQ�����˶�ʱ��Ϊt��t��0���룮���� ��1�����ɹ��ɶ������AC����֤����APQ�ס�ABC���ó���Ӧ�߳ɱ��������ɵó������
�ڹ���P��PH��AB�ڵ�H��AP=t��AQ=3-t��֤��AHP�ס�ABC�����PH=$\frac{4}{5}$t�����������������ʽ������ɣ�
��2���ٸ����߶εĴ�ֱƽ���ߵ��������AP=AQ���ó�3-t=t��������ɣ��ӳ�QP��AD�ڵ�E������Q��QO��AD��AC�ڵ�O��֤��AQO�ס�ABC�����AO��QO��PO=1��֤��APE�ס�OPQ���AE���ɣ�
�ڣ���������Q��B��A�˶�ʱl������B�����CP=AP=$\frac{1}{2}$AC=2.5���������t��
����������Q��A��B�˶�ʱl������B�����BP=BQ=6-t��AP=t��PC=5-t������P��PG��CB�ڵ�G��֤��PGC�ס�ABC�����PG=$\frac{3}{5}$��5-t����CG=$\frac{4}{5}$��5-t����BG=$\frac{4}{5}$t���ɹ��ɶ����ó����̣�������̵Ľ⼴�ɣ�
��� �⣺��1���١��ı���ABCD�Ǿ��Σ�
���B=90�㣬
��AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5��
��PQ��AC��
���APQ=90��=��B��
�֡ߡ�PAQ=��BAC��
���APQ�ס�ABC��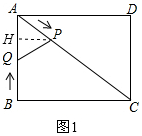
��$\frac{AP}{AB}=\frac{AQ}{AC}$��
��$\frac{t}{3}=\frac{3-t}{5}$��
��ã�t=$\frac{9}{8}$��
��t=$\frac{9}{8}$ʱ��PQ��AC��
�ʴ�Ϊ��$\frac{9}{8}$��
����ͼ1��ʾ������P��PH��AB�ڵ�H��AP=t��AQ=3-t��
���AHP=��ABC=90�㣬
�ߡ�PAH=��CAB��
���AHP�ס�ABC��
��$\frac{AP}{AC}=\frac{PH}{BC}$��
��AP=t��AC=5��BC=4��
��PH=$\frac{4}{5}$t��
��S=$\frac{1}{2}$•��3-t��•$\frac{4}{5}$t��
��S=-$\frac{2}{5}$t2+$\frac{6}{5}$t��t��ȡֵ��Χ�ǣ�0��t��3��
��2������ͼ2���߶�PQ�Ĵ�ֱƽ����Ϊl������A����AP=AQ��
��3-t=t��
��t=1.5��
��AP=AQ=1.5��
�ӳ�QP��AD�ڵ�E������Q��QO��AD��AC�ڵ�O��
���AQO�ס�ABC��
��$\frac{AO}{AC}=\frac{AQ}{AB}=\frac{QO}{BC}$��
��AO=$\frac{AQ}{AB}$•AC=$\frac{5}{2}$��QO=$\frac{AQ}{AB}$•BC=2��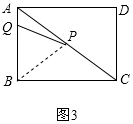
��PO=AO-AP=1��
��OQ��BC��AD��
���APE�ס�OPQ
��$\frac{AE}{QO}=\frac{AP}{QP}$��
��AE=$\frac{AP}{QP}$•QO=3��
�ڣ�������ͼ3������Q��B��A�˶�ʱl������B��
BQ=CP=AP=t����QBP=��QAP
�ߡ�QBP+��PBC=90�㣬��QAP+��PCB=90��
���PBC=��PCB CP=BP=AP=t
��CP=AP=$\frac{1}{2}$AC=$\frac{1}{2}$��5=2.5��t=2.5��
��������ͼ4������Q��A��B�˶�ʱl������B��
BP=BQ=3-��t-3��=6-t��AP=t��PC=5-t��
����P��PG��CB�ڵ�G����PG��AB��
���PGC�ס�ABC��
��$\frac{PC}{AC}=\frac{PG}{AB}=\frac{GC}{BC}$��
��PG=$\frac{PC}{AC}$•AB=$\frac{3}{5}$��5-t����CG=$\frac{PC}{AC}$•BC=$\frac{4}{5}$��5-t����
��BG=4-$\frac{4}{5}$��5-t��=$\frac{4}{5}$t��
�ɹ��ɶ����ã�BP2=BG2+PG2��
����6-t��2=��$\frac{4}{5}$t��2+[$\frac{3}{5}$��5-t��]2��
��ã�t=$\frac{45}{14}$��
��������������t��ֵ��ʹ��ֱ��l������B��t��ֵ��2.5��$\frac{45}{14}$��
���� �������ı����ۺ���Ŀ�������˾������ʣ��������������ʣ��߶δ�ֱƽ�������ʣ����ɶ��������������ε����ʺ��ж���Ӧ�ã���Ҫ����ѧ����������ͽ���������������Ŀ�Ƚϵ��ͣ�������һ�����Ѷȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��һũ��Ҫ��һ�����λ��ԣ����Ե�һ�����ó�Ϊ12m��ס��ǽ������������25m�������Χ�ɣ�Ϊ����������ڴ�ֱ��ס��ǽ��һ����һ��1m�����ţ��������Ϊ80m2������ǽ��ֱ��һ�߳�Ϊxm���ѱ�ע��ͼ�У���������г�����x�ķ����ǣ�������
��ͼ��һũ��Ҫ��һ�����λ��ԣ����Ե�һ�����ó�Ϊ12m��ס��ǽ������������25m�������Χ�ɣ�Ϊ����������ڴ�ֱ��ס��ǽ��һ����һ��1m�����ţ��������Ϊ80m2������ǽ��ֱ��һ�߳�Ϊxm���ѱ�ע��ͼ�У���������г�����x�ķ����ǣ�������| A�� | x��26-2x��=80 | B�� | x��24-2x��=80 | C�� | ��x-1����26-2x��=80 | D�� | x��25-2x��=80 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����x����Ϸ���ֱ�ǡ�BOA��ԭ��O˳ʱ�뷽����ת������BOA�����߷ֱ��뺯��y=-$\frac{1}{x}$��y=$\frac{2}{x}$��ͼ����B��A���㣬��tanA=$\frac{\sqrt{2}}{2}$��
��ͼ����x����Ϸ���ֱ�ǡ�BOA��ԭ��O˳ʱ�뷽����ת������BOA�����߷ֱ��뺯��y=-$\frac{1}{x}$��y=$\frac{2}{x}$��ͼ����B��A���㣬��tanA=$\frac{\sqrt{2}}{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
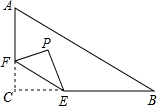 ��ͼ����Rt��ABC�У���C=90�㣬AC=3��BC=4����F�ڱ�AC�ϣ�����CF=1����EΪ��BC�ϵĶ��㣬����CEF��ֱ��EF���ۣ���C���ڵ�P�������P����AB�������Сֵ��$\frac{3}{5}$��
��ͼ����Rt��ABC�У���C=90�㣬AC=3��BC=4����F�ڱ�AC�ϣ�����CF=1����EΪ��BC�ϵĶ��㣬����CEF��ֱ��EF���ۣ���C���ڵ�P�������P����AB�������Сֵ��$\frac{3}{5}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
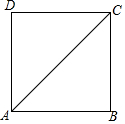 ��ͼ��������ABCD�ĶԽ���AC��Ϊ2$\sqrt{2}$����ֱ�����㣺�ٵ�C��ֱ��l�ľ���Ϊ1����B��D���㵽ֱ��l�ľ�����ȣ���ô���������ֱ��l��4����
��ͼ��������ABCD�ĶԽ���AC��Ϊ2$\sqrt{2}$����ֱ�����㣺�ٵ�C��ֱ��l�ľ���Ϊ1����B��D���㵽ֱ��l�ľ�����ȣ���ô���������ֱ��l��4�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com