
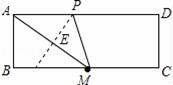
如图,在矩形ABCD中,AB=5,BC=24,M是BC的中点,若点P为线段AD上的一点,连接AM、PM,△PAM是以AP为腰的等腰三角形,则AP的长为 .


13或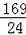
 .
.
【考点】矩形的性质;等腰三角形的判定;勾股定理.
【专题】分类讨论.
【分析】分两种情况:①当AP=AM时,根据勾股定理求出AM即可得出AP;
(2)当AP=MP时,P在AM的垂直平分线上,证明△PEA∽△ABM,得出对应边成比例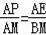
 ,即可求出AP.
,即可求出AP.
【解答】解:分两种情况:①当AP=AM时,
∵四边形ABCD是矩形,
∴∠B=∠BAD=90°,AD∥BC,
∵M是BC的中点,
∴BM=
 BC=12,
BC=12,
∴AM=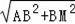
 =
=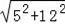
 =13,
=13,
∴AP=13;
(2)当AP=MP时,P在AM的垂直平分线上,如图所示:
则∠AEP=90°=∠B,AE=
 AM=
AM=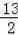
 ,
,
∵AD∥BC,
∴∠PAE=∠AMB,
∴△PEA∽△ABM,
∴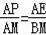
 ,即
,即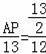
 ,
,
解得:AP=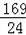
 ;
;
故答案为:13或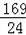
 .
.

【点评】本题考查了矩形的性质、等腰三角形的性质、勾股定理以及相似三角形的判定与性质;熟练掌握矩形的性质,并能进行推理计算是解决问题的关键.


科目:初中数学 来源: 题型:
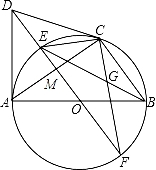
如图,AB是⊙O的直径,CD与⊙O相切于点C,DA⊥AB,DO及DO的延长线与⊙O分别相交于点E、F,EB与CF相交于点G.
(1)求证:DA=DC;
(2)⊙O的半径为3,AC= ,求GC的长.
,求GC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
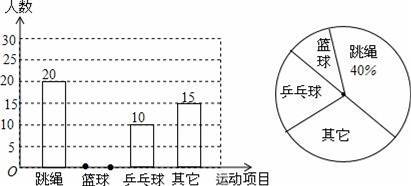
为了让学生更好地进行体育锻炼,某校开展了“大课间”体育活动.为便于管理与场地安排,学校以小明所在班级为例,对学生参加各个体育项目进行了调查统计.并把调查的结果绘制了如下图所示的不完全统计图,请你根据下列信息回答问题:
(1)在这次调查中,小明所在的班级参加篮球项目的同学有多少人?并补全条形统计图.
(2)如果学校有800名学生,请估计全校学生中有多少人参加篮球项目.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com