
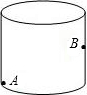
 有一圆柱形食品盒,它的高等于8cm,底面直径为$\frac{18}{π}$cm,蚂蚁爬行的速度为2cm/s.如果在盒内下底面的A处有一只蚂蚁,它想吃到盒内对面中部点B处的食物,那么它至少需要多少时间?(盒的厚度和蚂蚁的大小忽略不计,结果可含根号)
有一圆柱形食品盒,它的高等于8cm,底面直径为$\frac{18}{π}$cm,蚂蚁爬行的速度为2cm/s.如果在盒内下底面的A处有一只蚂蚁,它想吃到盒内对面中部点B处的食物,那么它至少需要多少时间?(盒的厚度和蚂蚁的大小忽略不计,结果可含根号) 科目:初中数学 来源: 题型:解答题
 如图是一套小户型经济房子的平面图尺寸
如图是一套小户型经济房子的平面图尺寸查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{25}$=±5 | B. | $\sqrt{(-5)^{2}}$=5 | C. | $\sqrt{16\frac{1}{4}}$=4$\frac{1}{2}$ | D. | $\root{3}{-8}$=2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
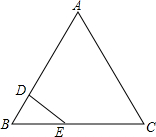 如图,等边△ABC的边长为4cm,点D从B点出发,沿BA方向运动到点A,到点A停止运动,点E从B点出发,沿BC方向运动,点D,E的速度分别为1cm/s,2cm/s,它们同时出发且同时停止,设它们运动的时间为t秒.
如图,等边△ABC的边长为4cm,点D从B点出发,沿BA方向运动到点A,到点A停止运动,点E从B点出发,沿BC方向运动,点D,E的速度分别为1cm/s,2cm/s,它们同时出发且同时停止,设它们运动的时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com