
分析 (1)利用根的判别式即可得出结论;
(2)根据y1的图象与x轴有一个交点的横坐标a满足5<a<7可知当x=5时,y1<0,当x=7时,y1>0求出m的取值范围,再由m为整数即可求出m的值;
(3)先求出当x=3,x=4时y1的值,再由y2也经过此点即可得出结论.
解答 解:(1)∵△=[-(m+3)]2-4(m+2)=(m+1)2≥0,
∴方程x2-(m+3)x+m+2=0必有实根;
(2)∵y1的图象与x轴有一个交点的横坐标a满足5<a<7,且抛物线开口向上,
∴f(5)<0,f(7)>0,
∴$\left\{\begin{array}{l}25-5(m+3)+m+2<0\\ 49-7(m+3)+m+2<0\end{array}\right.$,解得3<m<5.
∵m为整数,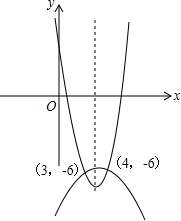
∴m=4;
(3)∵由(2)知,m=4,
∴关于x的二次函数y1=x2-(m+3)x+m+2可化为y1=x2-7x+6,
∴当x=3时,y1=-6;当x=4时,y1=-6.
∵二次函数y2=-x2+bx+c经过(3,-6),(4,-6),
∴$\left\{\begin{array}{l}{-6=-{3}^{2}+3b+c}\\{-6=-{4}^{2}+4b+c}\end{array}\right.$,解得$\left\{\begin{array}{l}{b=7}\\{c=-18}\end{array}\right.$,
∴y2的解析式为y2=-x2+7x-18.
点评 本题考查的是二次函数与不等式组,能根据题意画出图形,利用数形结合求解是解答此题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 摸到大王与摸到小王 | B. | 摸到红桃与摸到黑桃 | ||
| C. | 摸到点5与摸到点6 | D. | 摸到点5与摸到王牌 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
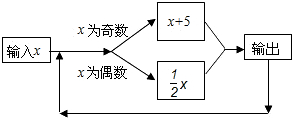 按如图所示的程序计算,若开始输入的x的值为48,我们发现第一次得到的结果为24,第2次得到的结果为12,…,请你探索第2013次得到的结果是( )
按如图所示的程序计算,若开始输入的x的值为48,我们发现第一次得到的结果为24,第2次得到的结果为12,…,请你探索第2013次得到的结果是( )| A. | 2 | B. | 4 | C. | 3 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
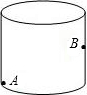 有一圆柱形食品盒,它的高等于8cm,底面直径为$\frac{18}{π}$cm,蚂蚁爬行的速度为2cm/s.如果在盒内下底面的A处有一只蚂蚁,它想吃到盒内对面中部点B处的食物,那么它至少需要多少时间?(盒的厚度和蚂蚁的大小忽略不计,结果可含根号)
有一圆柱形食品盒,它的高等于8cm,底面直径为$\frac{18}{π}$cm,蚂蚁爬行的速度为2cm/s.如果在盒内下底面的A处有一只蚂蚁,它想吃到盒内对面中部点B处的食物,那么它至少需要多少时间?(盒的厚度和蚂蚁的大小忽略不计,结果可含根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com