
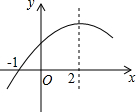 二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(-1,0),对称轴为
二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(-1,0),对称轴为分析 由抛物线的对称轴方程得到b=-4a>0,则可对①进行判断;由于x=-3时,y<0,则可对②进行判断;利用抛物线与x轴的一个交点为(-1,0)得a-b+c=0,把b=-4a代入可得c=-5a,则8a+7b+2c=-30a,于是可对③进行判断;根据而此函数的性质可对④进行判断.
解答 解:∵抛物线的对称轴为直线x=-$\frac{b}{2a}$=2,
∴b=-4a>0,即4a+b=0,所以①正确;
∵x=-3时,y<0,
∴9a-3b+c<0,即9a+c<3b,所以②错误;
∵抛物线与x轴的一个交点为(-1,0),
∴x=-1时,a-b+c=0,
∴a+4a+c=0,
∴c=-5a,
∴8a+7b+2c=8a-28a-10a=-30a,
而a<0,
∴8a+7b+2c>0,所以③正确;
∵抛物线的对称轴为直线x=2,
∴当x<2时,函数值随x增大而增大,所以④错误.
故答案为①③.
点评 本题考查了二次函数图象与系数的关系:对于二次函数y=ax2+bx+c(a≠0),a决定抛物线的开口方向和大小,当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右;常数项c决定抛物线与y轴交点:抛物线与y轴交于(0,c);抛物线与x轴交点个数由△决定:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:选择题
| A. | 41 | B. | 47 | C. | 50 | D. | 58 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
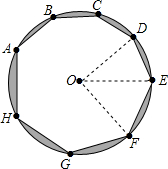 同圆或等圆中,圆心角互余的两个扇形叫做互余共轭扇形.如图⊙O内接八边形中,已知AB=BC=CD=DE=2,EF=FG=GH=HA=2$\sqrt{2}$.
同圆或等圆中,圆心角互余的两个扇形叫做互余共轭扇形.如图⊙O内接八边形中,已知AB=BC=CD=DE=2,EF=FG=GH=HA=2$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 在4×4的方格中有五个同样大小的正方形按图示位置摆放,移动其中一个正方形到空白方格中,与其余四个正方形组成的新图形是一个轴对称图形,这样的移法有( )个.
在4×4的方格中有五个同样大小的正方形按图示位置摆放,移动其中一个正方形到空白方格中,与其余四个正方形组成的新图形是一个轴对称图形,这样的移法有( )个.| A. | 8 | B. | 10 | C. | 12 | D. | 13 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com