
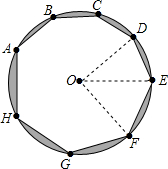
 同圆或等圆中,圆心角互余的两个扇形叫做互余共轭扇形.如图⊙O内接八边形中,已知AB=BC=CD=DE=2,EF=FG=GH=HA=2$\sqrt{2}$.
同圆或等圆中,圆心角互余的两个扇形叫做互余共轭扇形.如图⊙O内接八边形中,已知AB=BC=CD=DE=2,EF=FG=GH=HA=2$\sqrt{2}$.分析 (1)求出∠DOE和∠EOF的度数,相加为90°即可;
(2)FM⊥DE的延长线于M,判断出△DOF是等腰直角三角形,求出OD的长,即为半径;
(3)分别作OP⊥DE于P;OQ⊥EF于Q,根据S阴影=[S扇形EOF-(S△DOE+S△EOF)]×4,即可解答.
解答 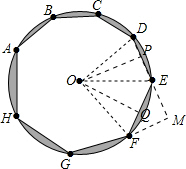 解:(1)∵AB=BC=CD=DE=2,EF=FG=GH=HA=2$\sqrt{2}$,
解:(1)∵AB=BC=CD=DE=2,EF=FG=GH=HA=2$\sqrt{2}$,
∴∠DOE=$\frac{2}{4×2+4×2\sqrt{2}}$×360°=( $\sqrt{2}$-1)•90°;∠EOF=$\frac{2\sqrt{2}}{2\sqrt{2}×4+2×4}$×360°=(2-$\sqrt{2}$)•90°
∴∠DOE+∠EOF=($\sqrt{2}$-1)•90°+(2-$\sqrt{2}$)•90°=90°,
∴扇形DOE与扇形EOF为互余共轭扇形.
(2)如图所示,FM⊥DE的延长线于M,
由(1)知∠DOF=∠DOE+∠EOF=(180°-2∠DEO)+(180°-2FEO)=360°-2∠DEF=90°
∴∠DEF=135°;
∴∠FEM=45°,
∴△EMF是等腰直角三角形
∴ME=MF=$\frac{\sqrt{2}}{2}$EF=$\frac{\sqrt{2}}{2}$×2$\sqrt{2}$=2;DM=DE+ME=2+2=4,
在Rt△DMF中:DF=$\sqrt{{DM}^{2}+{MF}^{2}}$=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,
∵OD=OF;∠DOF=90°,
∴△DOF是等腰直角三角形,
∴OD=OF=$\frac{\sqrt{2}}{2}$DF=$\frac{\sqrt{2}}{2}$×2$\sqrt{5}$=$\sqrt{10}$;即⊙O的半径为$\sqrt{10}$;
(3)如图所示,分别作OP⊥DE于P;OQ⊥EF于Q,
∴OP=$\sqrt{{OD}^{2}-(\frac{1}{2}DE)^{2}}$=$\sqrt{10-1}$=3,OQ=$\sqrt{{OF}^{2}-(\frac{1}{2}EF)^{2}}$=$\sqrt{10-2}$=2$\sqrt{2}$,
∴S△DOE=$\frac{1}{2}$DE•OP=$\frac{1}{2}$×2×3=3;
S△EOF=$\frac{1}{2}$×EF•OQ=$\frac{1}{2}$×2$\sqrt{2}$×2$\sqrt{2}$=4,
S扇形EOF=$\frac{1}{4}$πOD2=$\frac{5}{2}$π,
∴S阴影=[S扇形EOF-(S△DOE+S△EOF)]×4=[$\frac{5}{2}$π-(4+3)]×4=10π-28.
点评 本题考查学生对正多边形的概念掌握和计算的能力.解答这类题往往一些学生因对正多边形的基本知识不明确,将多边形的半径与内切圆的半径相混淆而造成错误计算.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
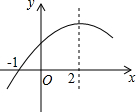 二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(-1,0),对称轴为
二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(-1,0),对称轴为查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com