
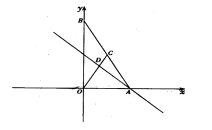
【题目】如图,在平面直角坐标系中,点A、B分别在x轴、y轴上,线段OA、OB的长(OA<OB)是方程组![]() 的解,点C是直线
的解,点C是直线![]() 与直线AB的交点,点D在线段OC上,OD=
与直线AB的交点,点D在线段OC上,OD=![]()
(1)求点C的坐标;
(2)求直线AD的解析式;
(3)P是直线AD上的点,在平面内是否存在点Q,使以O、A、P、Q为顶点的四边形是菱形(邻边相等的平行四边形)?若存在,请写出点Q的坐标;若不存在,请说明理由.
【答案】(1)C点的坐标是(3,6);(2)AD的函数解析式为y=x+6;(3)Q1(3![]() ,3
,3![]() )、Q2(3
)、Q2(3![]() ,3
,3![]() )、Q3(6,6)、Q4(3,3).
)、Q3(6,6)、Q4(3,3).
【解析】
(1)根据解方程组,可得A、B的坐标,根据待定系数法,可得函数解析式,根据解方程组,可得点C的坐标;
(2)根据D在OC上,OD=![]() ,可得方程组,根据解方程组,可得D点坐标,根据待定系数法,可得AD的函数解析式;
,可得方程组,根据解方程组,可得D点坐标,根据待定系数法,可得AD的函数解析式;
(3)结合菱形的性质,分情况讨论:若P在x轴上方,若P在x轴下方,若Q在x轴上方,若Q在x轴下方,进行计算即可得到答案.
(1)解![]() ,得
,得![]() ,即A(6,0)、B(0,12).设直线AB的解析式y=kx+b,把A、B点的坐标代入函数解析式,得
,即A(6,0)、B(0,12).设直线AB的解析式y=kx+b,把A、B点的坐标代入函数解析式,得![]() ,解得
,解得![]() .直线AB的解析式y=2x+12,由点C是直线y=2x与直线AB的交点,得
.直线AB的解析式y=2x+12,由点C是直线y=2x与直线AB的交点,得![]() ,解得
,解得![]() ,C点的坐标是(3,6);
,C点的坐标是(3,6);
(2)由点D在线段OC上,OD=![]() ,
,
得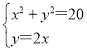 ,解得
,解得![]() ,即D点坐标是(2,4)
,即D点坐标是(2,4)
设AD的函数解析式为y=kx+b,把A、D点的坐标代入,得![]()
,解得![]() .
.
AD的函数解析式为y=x+6;
(3)过D作DF⊥x轴,由(2)中D的坐标可知,则DF=AF=4,所以∠OAD=45°,因为以O、A、P、Q为顶点的四边形是菱形,所以需分情况讨论:
若P在x轴上方,OAPQ是菱形,则PQ∥OA,PQ=OA=/span>6=AP,过P作PM⊥x轴,
如图所示,

因为∠OAD=45°,由三角函数可得PM=AM=![]() =3
=3![]() ,OM=63
,OM=63![]() ,即P(63
,即P(63![]() ,3
,3![]() ),
),
所以Q的横坐标为63![]() 6=3
6=3![]() ,Q1(3
,Q1(3![]() ,3
,3![]() );
);
若P在x轴下方,OAPQ是菱形,则PQ∥OA,PQ=OA=6=AP.过P作PM⊥x轴,
如图所示,
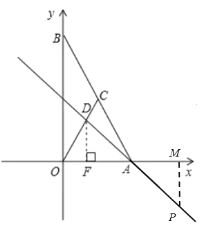
因为∠MAP=∠OAD=45°,由三角函数得到PM=AM=![]() =3
=3![]() ,OM=6+3
,OM=6+3![]() ,即P(6+3
,即P(6+3![]() ,3
,3![]() ),
),
所以Q的横坐标为6+3![]() 6=3
6=3![]() ,Q2(3
,Q2(3![]() ,3
,3![]() );
);
若Q在x轴上方,OAQP是菱形,则∠OAQ=2∠OAD=90°,所以此时OAQP是正方形.
又因正方形边长为6,所以此时Q3(6,6);
若Q在x轴下方,OPAQ是菱形,则∠PAQ=2∠OAD=90°,
所以此时OPAQ是正方形.又因正方形对角线为6,
由正方形的对称性可得Q4(3,/span>3).


科目:初中数学 来源: 题型:
【题目】学校有一批复印任务,原来由甲复印社承接,按每100页40元计费.现乙复印社表示:若学校先按月付给一定数额的承包费,则可按每100页15元收费.两复印社每月收费情况如图所示.根据图象回答:
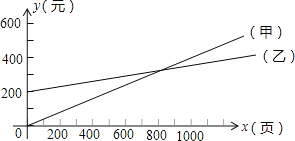
(1)设两家复印社每月复印任务为![]() 张,分别求出甲复印社的每月复印收费y甲(元)与乙复印社的每月复印收费y乙(元)与复印任务
张,分别求出甲复印社的每月复印收费y甲(元)与乙复印社的每月复印收费y乙(元)与复印任务![]() (张)之见的函数关系式.
(张)之见的函数关系式.
(2)乙复印社的每月承包费是多少?
(3)当每月复印多少页时,两复印社实际收费相同?
(4)如果每月复印页数是1200页,那么应选择哪个复印社.
查看答案和解析>>
科目:初中数学 来源: 题型:
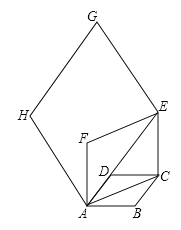
【题目】如图,边长为![]() 的菱形
的菱形![]() 中,
中,![]() .连结对角线
.连结对角线![]() ,以
,以![]() 为边作第二个菱形
为边作第二个菱形![]() ,使
,使![]() .连结
.连结![]() ,再以
,再以![]() 为边作第三个菱形
为边作第三个菱形![]() ,使
,使![]() ,一按此规律所作的第
,一按此规律所作的第![]() 个菱形的边长是__________.
个菱形的边长是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).
(1)把△ABC沿BA方向平移后,点A移到点A1,在网格中画出平移后得到的△A1B1C1;
(2)把△A1B1C1绕点A1按逆时针方向旋转90°,在网格中画出旋转后的△A1B2C2;
(3)如果网格中小正方形的边长为1,求点B经过(1)、(2)变换的路径总长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】鄂州市化工材料经销公司购进一种化工原料若干千克,价格为每千 克30元.物价部门规定其销售单价不高于每千克60元,不低于每千克30元.经市场调查发现:日销售量y(千克)是销售单价x(元)的一次函数,且当x=60时 ,y=80;x=50时,y=100.在销售过程中,每天还要支付其他费用450元.
(1)(3分)求出y与x的函数关系式,并写出自变量x的取值范围.
(2)(3分)求该公司销售该原料日获利w(元)与销售单价x(元)之间的函数关系式.
(3)(4分)当销售单价为多少元时,该公司日获利最大?最大获利是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年“清明节”前夕,宜宾某花店用1000元购进若干菊花,很快售完,接着又用2500元购进第二批
花,已知第二批所购花的数量是第一批所购花数的2倍,且每朵花的进价比第一批的进价多![]() 元.
元.
(1)第一批花每束的进价是多少元.
(2)若第一批菊花按3元的售价销售,要使总利润不低于1500元(不考虑其他因素),第二批每朵菊花的售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
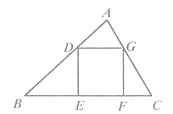
【题目】如图,△ABC中,正方形DEFG的顶点D,G分别在AB,AC上,顶点E,F在BC上.若△ADG、△BED、△CFG的面积分别是1、3、1,则正方形的边长为( )
A. ![]() B.
B. ![]() C. 2 D. 2
C. 2 D. 2![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com