
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(﹣2,6),且与x轴相交于点B,与正比例函数y=3x的图象相交于点C,点C的横坐标为1.
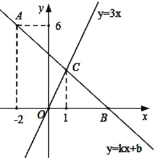
(1)求k、b的值;
(2)请直接写出不等式kx+b>3x中x的范围.
(3)若点D在y轴上,且满足S△BCD=2S△BOC,求点D的坐标.
【答案】(1)k=-1,b=4;(2)x<1;(3)点D的坐标为(0,12)或(0,-4).
【解析】
(1)将x=1代入y=3x中可求得点C坐标,继而结合点A坐标利用待定系数法即可求得k、b的值;
(2)结合函数图象可知不等式的解集即为直线y=kx+b在直线y=3x上方的部分对应的x的取值范围,结合点C坐标即可求得答案;
(3)先求出S△BOC的值,然后分点D在y轴正半轴与负半轴两种情况结合三角形面积公式进行求解即可.
(1)当x=1时,y=3x=3,
∴点C的坐标为(1,3),
将A(﹣2,6)、C(1,3)代入y=kx+b,
得:![]() ,
,
解得:![]() ;
;
(2)观察图象可知,当x<1时,kx+b>3x,
所以不等式kx+b>3x的解集是x<1;
(3)由(1)知一次函数y=kx+b为y=-x+4,
当y=0时,有﹣x+4=0,
解得:x=4,
∴点B的坐标为(4,0),
∵点C(1,3),
∴S△BOC=![]() =6,
=6,
设点D的坐标为(0,m),
如图1,当点D在y轴正半轴上时,
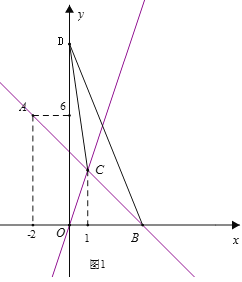
S△DBC=S△DOB-S△DCO-S△BOC=![]() ,
,
∵S△BCD=2S△BOC,
∴![]() =6×2,
=6×2,
∴m=12,
∴点D的坐标为(0,12);
如图2,当点D在y轴负半轴上时,
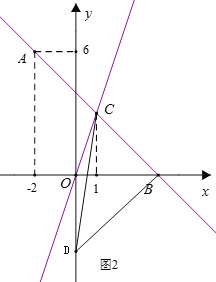
S△DBC=S△DOB+S△BOC-S△DCO =![]() ,
,
∵S△BCD=2S△BOC,
∴![]() =6×2,
=6×2,
∴m=-4,
∴点D的坐标为(0,-4),
综上,点D的坐标为(0,12)或(0,-4).


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:初中数学 来源: 题型:
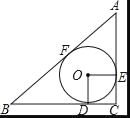
【题目】如图,△ABC中,∠C=90°,⊙O是△ABC的内切圆,D、E、F是切点.
(1)求证:四边形ODCE是正方形;
(2)如果AC=6,BC=8,求内切圆⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,∠C=90°,按以下步骤:①分别以A.B为圆心,以大于![]() AB的长为半径作弧,两弧相交于两点M、N;②作直线MN交BC于点D. 若AC=1.5,∠B=15°.则BD等于( )
AB的长为半径作弧,两弧相交于两点M、N;②作直线MN交BC于点D. 若AC=1.5,∠B=15°.则BD等于( )

A.1.5B.2C.2.5D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图△ABC中,∠ABC=45°,AB=BC,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F.H是BC边的中点,连接DH与BE相交于点G,

(1)求证BF=AC;
(2)求证CE=![]() BF.
BF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=m°,∠ABC和∠ACD的平分线交于点A1,得∠A1,∠A1BC和∠A1CD的平分线交于点A2,得∠A2…∠A2 017BC和∠A2 017CD的平分线交于点A2 018,则∠A2 018=_____度.
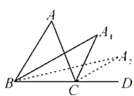
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,AB=2,∠ABC=30°,点E是射线DA上一动点,把△CDE沿CE折叠,其中点D的对应点为点D′,若CD′垂直于菱形ABCD的边时,则DE的长为_____.
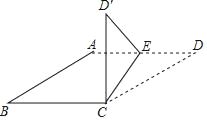
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com