
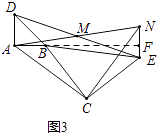
����Ŀ����ͼ����֪��BAD�͡�BCE��Ϊ����ֱ�������Σ���BAD=��BCE=90�㣬��MΪDE���е㣬����E��ADƽ�е�ֱ�߽�����AM�ڵ�N��
��1����A��B��C������ͬһֱ����ʱ����ͼ1������֤��MΪAN���е㣻 
��2����ͼ1�еġ�BCE�Ƶ�B��ת����A��B��E������ͬһֱ����ʱ����ͼ2������֤����ACNΪ����ֱ�������Σ� 
��3����ͼ1�С�BCE�Ƶ�B��ת��ͼ3λ��ʱ����2���еĽ����Ƿ��Գ���������������֤��֮��������������˵�����ɣ� 
���𰸡�
��1��֤������ͼ1��
��EN��AD��
���MAD=��MNE����ADM=��NEM��
�ߵ�MΪDE���е㣬
��DM=EM��
�ڡ�ADM�͡�NEM�У�
�� 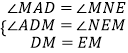 ��
��
���ADM�ա�NEM��
��AM=MN��
��MΪAN���е㣮
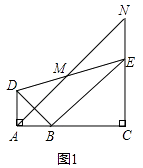
��2��֤������ͼ2��
�ߡ�BAD�͡�BCE��Ϊ����ֱ�������Σ�
��AB=AD��CB=CE����CBE=��CEB=45�㣮
��AD��NE��
���DAE+��NEA=180�㣮
�ߡ�DAE=90�㣬
���NEA=90�㣮
���NEC=135�㣮
��A��B��E������ͬһֱ���ϣ�
���ABC=180�㩁��CBE=135�㣮
���ABC=��NEC��
�ߡ�ADM�ա�NEM����֤����
��AD=NE��
��AD=AB��
��AB=NE��
�ڡ�ABC�͡�NEC�У�
���ABC�ա�NEC��
��AC=NC����ACB=��NCE��
���ACN=��BCE=90�㣮
���ACNΪ����ֱ�������Σ�
��3����ACN��Ϊ����ֱ�������Σ�
֤������ͼ3���ӳ�AB��NE�ڵ�F��
��AD��NE��MΪ�е㣬
���á�ADM�ա�NEM��
��AD=NE��
��AD=AB��
��AB=NE��
��AD��NE��
��AF��NE��
���ı���BCEF�У�
�ߡ�BCE=��BFE=90��
���FBC+��FEC=360�㩁180��=180��
�ߡ�FBC+��ABC=180��
���ABC=��FEC
�ڡ�ABC�͡�NEC�У�
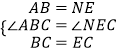
���ABC�ա�NEC��
��AC=NC����ACB=��NCE��
���ACN=��BCE=90�㣮
���ACNΪ����ֱ�������Σ�
����������1����EN��AD�͵�MΪDE���е����֤����ADM�ա�NEM���Ӷ�֤��MΪAN���е㣮��2����֤AB=DA=NE����ABC=��NEC=135�㣬�Ӷ�����֤����ABC�ա�NEC����������֤��AC=NC����ACN=��BCE=90�㣬���С�ACNΪ����ֱ�������Σ���3���ӳ�AB��NE�ڵ�F���á�ADM�ա�NEM�������ı���BCEF�ڽǺͣ��ɵá�ABC=��FEC���Ӷ�����֤����ABC�ա�NEC����������֤��AC=NC����ACN=��BCE=90�㣬���С�ACNΪ����ֱ�������Σ�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����������ת����ת�̱�3�ȷ֣�ָ������ÿ�������ڵĻ�����ȣ� 
��1�������ת��ת��һ�Σ�ֹͣ��ָ��ָ��1�ĸ���Ϊ��
��2��С����С���������ת������Ϸ��������������Ϸ��������Ϊ��˫����ƽ�������б�����״ͼ�ķ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ȫ�ȵĺ�30��ǵ�ֱ�������Σ� 
��1��������ȱ�ƴ��һ�����һ��û���ص����ֵ�ƽ��ͼ�Σ����㻭�����в�ͬ��ƴ��ƽ��ͼ�ε�ʾ��ͼ��
��2��������1����ƽ��ͼ�ηֱ�ӡ�����ʵء���״����С��ȫ��ͬ�Ŀ�Ƭ�ϣ�ϴ�Ⱥ���������ȡһ�ţ����ȡ�Ŀ�Ƭ��ƽ��ͼ��Ϊ��Գ�ͼ�εĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǰ�ԲO��ֱ����C��D�ǰ�ԲO�ϵ����㣬��OD��BC��OD��AC���ڵ�E�� 
��1������B=70�㣬���CAD�Ķ�����
��2����AB=4��AC=3����DE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������һ��������һ���ǵ�3������ô���dz����������Ϊ���ǻ������Ρ������и��������У�����Ϊһ���ǻ����������߳���һ���ǣ� ��
A.1��2��3
B.1��1�� ![]()
C.1��1�� ![]()
D.1��2�� ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����y=�� ![]() x+b��ͼ����x�ᡢy��ֱ��ڵ�A��B���뺯��y=x��ͼ���ڵ�M����M�ĺ�����Ϊ2����x������һ��P��a��0��������a��2��������P��x��Ĵ��ߣ��ֱ���y=��
x+b��ͼ����x�ᡢy��ֱ��ڵ�A��B���뺯��y=x��ͼ���ڵ�M����M�ĺ�����Ϊ2����x������һ��P��a��0��������a��2��������P��x��Ĵ��ߣ��ֱ���y=�� ![]() x+b��y=x��ͼ���ڵ�C��D��
x+b��y=x��ͼ���ڵ�C��D�� 
��1�����A�����ꣻ
��2����OB=CD����a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB��CD�ǡ�O��ֱ����BE�ǡ�O���ң���BE��CD������C��������EB���ӳ��߽��ڵ�P������BC�� 
��1����֤��BCƽ�֡�ABP��
��2����֤��PC2=PBPE��
��3����BE��BP=PC=4�����O�İ뾶��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com