
【题目】已知二次函数y=ax2+bx+c的图象经过点A(1,0).
(1)当b=2,c=﹣3时,求二次函数的解析式及二次函数最小值;
(2)二次函数的图象经过点B(m,e),C(3﹣m,e)且对任意实数x,函数值y都不小于![]() ﹣
﹣![]() .
.
①求此时二次函数的解析式;
②若次函数与y轴交于点D,在对称轴上存在一点P,使得PA+PD有最小值,求点P坐标及PA+PD的最小值.
【答案】(1)y=(x+1)2-4,当x=-1时,y最小值为-4;(2)①y=x2﹣3x+2,②存在,P(![]() ,
,![]() ),2
),2![]()
【解析】
(1)利用待定系数法以及配方法即可解决问题.
(2)①首先求出b、c(用a表示),想办法列出不等式即可解决问题.
②根据解析式求得对称轴,然后根据对称性求得A的对称点的坐标,连接A′D交抛物线的对称轴与点P.此时PA+PD=A′D,则PA+PD最小.
解:(1)将b=2,c=﹣3代入得:y=ax2+2x﹣3.
将点A(1,0)代入y=ax2+2x﹣3,得a+2﹣3=0,
∴a=1.
∴y=x2+2x﹣3,
∵y=(x+1)2﹣4,
∴当x=﹣1时,y最小值为﹣4.
(2)①由题意可知:对称轴![]() .
.
∴![]() ,
,
∴b=﹣3a,又∵a+b+c=0,
∴c=2a,
∴y=ax2﹣3ax+2a
顶点纵坐标为![]() ,
,
∵函数值y不小于![]() ﹣
﹣![]()
∴a>0,且![]() ,
,
∴a2﹣2a+1≤0,
∴(a﹣1)2≤0,
∵(a﹣1)2≥0,
∴a﹣1=0,
∴a=1.
∴抛物线的解析式为y=x2﹣3x+2;
②如图所示:
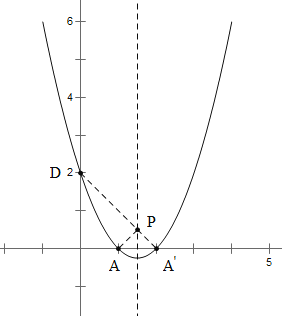
求得A关于对称轴的对称点A′的坐标,连接A′D交抛物线的对称轴与点P.此时PA+PD=A′D,则PA+PD最小,
∵y=x2﹣3x+2=(x﹣![]() )2﹣
)2﹣![]() ,
,
∴对称轴为直线x=![]() ,
,
∴A关于对称轴的对称点A′(2,0),
由y=x2﹣3x+2可知D(0,2),
设直线A′D的解析式为y=kx+n,
∴![]() 解得
解得![]()
∴直线A′D的解析式为y=﹣x+2,
把x=![]() 代入得,y=
代入得,y=![]() ,
,
∴P(![]() ,
,![]() ),
),
∵![]() ,
,
∴PA+PD的最小值为2![]()


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】国家计划2035年前实施新能源汽车,某公司为加快新旧动能转换,提高公司经济效益,决定对近期研发出的一种新型能源产品进行降价促销.根据市场调查:这种新型能源产品销售单价定为200元时,每天可售出300个;若销售单价每降低1元,每天可多售出5个.已知每个新型能源产品的成本为100元.
问:(1)设该产品的销售单价为![]() 元,每天的利润为
元,每天的利润为![]() 元.则
元.则![]() _________(用含
_________(用含![]() 的代数式表示)
的代数式表示)
(2)这种新型能源产品降价后的销售单价为多少元时,公司每天可获利32000元?
查看答案和解析>>
科目:初中数学 来源: 题型:
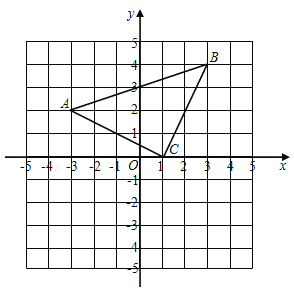
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为B(3,4)、A(﹣3,2)、C(1,0),正方形网格中,每个小正方形的边长是一个单位长度.
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格上画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为1:2,点C2的坐标是 ;(画出图形)
(3)若M(a,b)为线段AC上任一点,写出点M的对应点M2的坐标 .
查看答案和解析>>
科目:初中数学 来源: 题型:
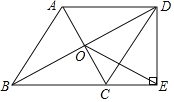
【题目】如图,在四边形ABCD中,AD∥BC,AB=BC,对角线AC、BD交于点O,BD平分∠ABC,过点D作DE⊥BC,交BC的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若DC=2![]() ,AC=4,求OE的长.
,AC=4,求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
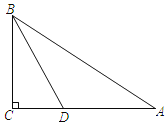
【题目】如图,在Rt△ABC中,∠ACB=90°,BD平分∠ABC.求作⊙O,使得点O在边AB上,且⊙O经过B、D两点;并证明AC与⊙O相切.(尺规作图,保留作图痕迹,不写作法)
查看答案和解析>>
科目:初中数学 来源: 题型:
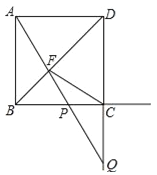
【题目】如图,正方形ABCD的边长为1,点P在射线BC上(异于点B、C),直线AP与对角线BD及射线DC分别交于点F、Q.
(1)若BP=![]() ,求∠BAP的度数;
,求∠BAP的度数;
(2)若点P在线段BC上,过点F作FG⊥CD,垂足为G,当△FGC≌△QCP时,求PC的长;
(3)以PQ为直径作⊙M.
①判断FC和⊙M的位置关系,并说明理由;
②当直线BD与⊙M相切时,直接写出PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
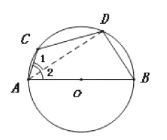
【题目】如图,AB是⊙0的直径,点C在⊙0上,D是![]() 中点,若∠BAC=70°,求∠C.
中点,若∠BAC=70°,求∠C.
下面是小雯的解法,请帮他补充完整:
解:在⊙0中,
∵D是![]() 的中点
的中点
∴BD=CD.
∴∠1=∠2( )(填推理的依据).
∵∠BAC=70°,
∴∠2=35°.
∵AB是⊙0的直径,
∴∠ADB=90°( )(填推理的依据).
∴∠B=90°-∠2=55°.
∵A、B、C、D四个点都在⊙0上,
∴∠C+∠B=180°( )(填推理的依据).
∴∠C=180°-∠B= (填计算结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
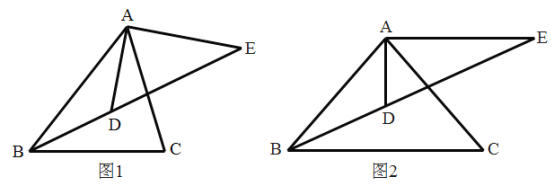
【题目】如图1,AD、BD分别是△ABC的内角∠BAC、∠ABC的平分线,过点A作AE⊥AD,交BD的延长线于点E.
(1)求证:∠E=![]() ∠C;
∠C;
(2)如图2,如果AE=AB,且BD:DE=2:3,求cos∠ABC的值;
(3)如果∠ABC是锐角,且△ABC与△ADE相似,求∠ABC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com