
【题目】在平面直角坐标系中,点A(0,4),B(m,0)在坐标轴上,点C,O关于直线AB对称,点D在线段AB上.
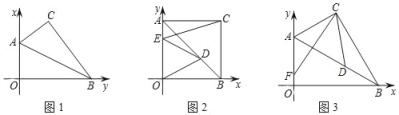
(1)如图1,若m=8,求AB的长;
(2)如图2,若m=4,连接OD,在y轴上取一点E,使OD=DE,求证:CE=![]() DE;
DE;
(3)如图3,若m=4![]() ,在射线AO上裁取AF,使AF=BD,当CD+CF的值最小时,请在图中画出点D的位置,并直接写出这个最小值.
,在射线AO上裁取AF,使AF=BD,当CD+CF的值最小时,请在图中画出点D的位置,并直接写出这个最小值.
【答案】(1)AB=4![]() ;(2)见解析;(3)CD+CF的最小值为4
;(2)见解析;(3)CD+CF的最小值为4![]() .
.
【解析】
(1)根据勾股定理可求AB的长;
(2)过点D作DF⊥AO,根据等腰三角形的性质可得OF=EF,根据轴对称的性质等腰直角三角形的性质可得AF=DF,设OF=EF=x,AE=4﹣2x,根据勾股定理用参数x表示
DE,CE的长,即可证CE=![]() DE;
DE;
(3)过点B作BM⊥OB,在BM上截取BM=AO,过点C作CN⊥BM,交MB的延长线于点N,根据锐角三角函数可得∠ABO=30°,根据轴对称的性质可得AC=AO=4,BO=BC=4![]() ,∠ABO=∠ABC=30°,∠OAB=∠CAB=60°,根据“SAS”可证△ACF≌△BMD,可得CF=DM,则当点D在CM上时,CF+CD的值最小,根据直角三角形的性质可求CN,BN的长,根据勾股定理可求CM的长,即可得CF+CD的最小值.
,∠ABO=∠ABC=30°,∠OAB=∠CAB=60°,根据“SAS”可证△ACF≌△BMD,可得CF=DM,则当点D在CM上时,CF+CD的值最小,根据直角三角形的性质可求CN,BN的长,根据勾股定理可求CM的长,即可得CF+CD的最小值.
(1)∵点A(0,4),B(m,0),且m=8,
∴AO=4,BO=8,
在Rt△ABO中,AB=![]()
(2)如图,过点D作DF⊥AO,
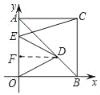
∵DE=DO,DF⊥AO,
∴EF=FO,
∵m=4,
∴AO=BO=4,
∴∠ABO=∠OAB=45°,
∵点C,O关于直线AB对称,
∴∠CAB=∠CBA=45°,AO=AC=OB=BC=4,
∴∠CAO=∠CBO=90°,
∵DF⊥AO,∠BAO=45°,
∴∠DAF=∠ADF=45°,
∴AF=DF,
设OF=EF=x,AE=4﹣2x,
∴AF=DF=4﹣x,
在Rt△DEF中,DE=![]()
在Rt△ACE中,CE=![]()
∴CE=![]() DE,
DE,
(3)如图,过点B作BM⊥OB,在BM上截取BM=AO,过点C作CN⊥BM,交MB的延长线于点N,
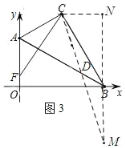
∵m=4![]() ,
,
∴OB=4![]() ,
,
∴tan∠ABO=![]() ,
,
∴∠ABO=30°
∵点C,O关于直线AB对称,
∴AC=AO=4,BO=BC=4![]() ,∠ABO=∠ABC=30°,∠OAB=∠CAB=60°,
,∠ABO=∠ABC=30°,∠OAB=∠CAB=60°,
∴∠CAF=120°,∠CBO=60°
∵BM⊥OB,∠ABO=30°,
∴∠ABM=120°,
∴∠CAF=∠ABM,且DB=AF,BM=AO=AC=4,
∴△ACF≌△BMD(SAS)
∴CF=DM,
∵CF+CD=CD+DM,
∴当点D在CM上时,CF+CD的值最小,
即CF+CD的最小值为CM的长,
∵∠CBO=60°,BM⊥OB,
∴∠CBN=30°,且BM⊥OB,BC=4![]() ,
,
∴CN=2![]() ,BN=
,BN=![]() CN=6,
CN=6,
∴MN=BM+BN=4+6=10,
在Rt△CMN中,CM=![]() ,
,
∴CD+CF的最小值为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图所示,小明在自家楼顶上的点A处测量建在与小明家楼房同一水平线上邻居的电梯的高度,测得电梯楼顶部B处的仰角为45°,底部C处的俯角为26°,已知小明家楼房的高度AD=15米,求电梯楼的高度BC(结果精确到0.1米)(参考数据:sin26°≈0.44,cos26°≈0.90,tan26°≈0.49)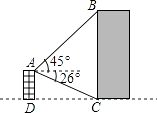
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个安装有进出水管的30升容器,水管单位时间内进出的水量是一定的,设从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,得到水量y(升)与时间x(分)之间的函数关系如图所示.根据图象信思给出下列说法,其中错误的是( )

A. 每分钟进水5升
B. 每分钟放水1.25升
C. 若12分钟后只放水,不进水,还要8分钟可以把水放完
D. 若从一开始进出水管同时打开需要24分钟可以将容器灌满
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D在AB上,点E在BC上,BD=BE.
(1)请你再添加一个条件,使得△BEA≌△BDC,并给出证明.你添加的条件是 .
(2)根据你添加的条件,再写出图中的一对全等三角形 .(只要求写出一对全等三角形,不再添加其他线段,不再标注或使用其他字母,不必写出证明过程)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线C1:y=x2+bx+c经过原点,与x轴的另一个交点为(2,0),将抛物线C1向右平移m(m>0)个单位得到抛物线C2 , C2交x轴于A,B两点(点A在点B的左边),交y轴于点C.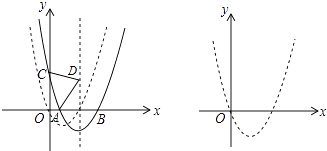
(1)求抛物线C1的解析式及顶点坐标;
(2)以AC为斜边向上作等腰直角三角形ACD,当点D落在抛物线C2的对称轴上时,求抛物线C2的解析式;
(3)若抛物线C2的对称轴存在点P,使△ PAC为等边三角形,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD∥BC,∠EAD=∠C.

(1)试判断AE与CD的位置关系,并说明理由;
(2)若∠FEC=∠BAE,∠EFC=50°,求∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
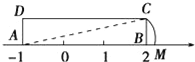
【题目】如图,矩形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴的正半轴于M,则点M的表示的数为________________.
【答案】![]()
【解析】AC=AM=![]() =
=![]() ,∴AM=
,∴AM=![]()
【题型】填空题
【结束】
11
【题目】在△ABC中,AB=10,AC=2![]() ,BC边上的高AD=6,则另一边BC等于_______.
,BC边上的高AD=6,则另一边BC等于_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:我们学过一次函数的图象的平移,如:将一次函数![]() 的图象沿x轴向右平移1个单位长度可得到函数
的图象沿x轴向右平移1个单位长度可得到函数![]() 的图象,再沿y轴向上平移1个单位长度,得到函数
的图象,再沿y轴向上平移1个单位长度,得到函数![]() 的图象;如果将一次函数
的图象;如果将一次函数![]() 的图象沿x轴向左平移1个单位长度可得到函数
的图象沿x轴向左平移1个单位长度可得到函数![]() 的图象,再沿y轴向下平移1个单位长度,得到函数
的图象,再沿y轴向下平移1个单位长度,得到函数![]() 的图象;仿照上述平移的规律,解决下列问题:
的图象;仿照上述平移的规律,解决下列问题:
![]() 将一次函数
将一次函数![]() 的图象沿x轴向右平移3个单位长度,再沿y轴向上平移1个单位长度,得到函数的图象;
的图象沿x轴向右平移3个单位长度,再沿y轴向上平移1个单位长度,得到函数的图象;
![]() 将
将![]() 的函数图象沿y轴向下平移3个单位长度,得到函数的图象,再沿x轴向左平移1个单位长度,得到函数的图象;
的函数图象沿y轴向下平移3个单位长度,得到函数的图象,再沿x轴向左平移1个单位长度,得到函数的图象;
![]() 函数
函数![]() 的图象可由
的图象可由![]() 的图象经过怎样的平移变换得到?
的图象经过怎样的平移变换得到?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,将矩形OABC置于平面直角坐标系中,点A,C分别在x,y轴的正半轴上,已知点B(4,2),将矩形OABC翻折,使得点C的对应点P恰好落在线段OA(包括端点O,A)上,折痕所在直线分别交BC、OA于点D、E;若点P在线段OA上运动时,过点P作OA的垂线交折痕所在直线于点 Q.设点Q的坐标为(x,y),则y关于x的函数关系式是 .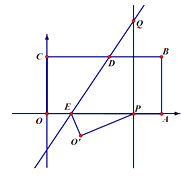
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com