
【题目】如图,D是△ABC的BC边上的一点,∠B =40°,∠ADC=80°.

(1)求证:AD=BD;
(2)若∠BAC=70°,判断△ABC的形状,并说明理由.
【答案】(1)证明见解析;(2)△ABC是等腰三角形,理由见解析.
【解析】试题解析:(1)由AD=BD,根据等边对等角的性质,可得∠B=∠BAD,又由三角形外角的性质,即可求得∠B的度数;
(2)由∠BAC=70°,易求得∠C=∠BAC=70°,根据等角对等边的性质,可证得△ABC是等腰三角形.
试题解析:(1)证明:∵∠ADC=∠B+∠BAD,而∠ADC=80°,∠B =40°,
∴∠BAD=80°-40°=40°,
∴∠B=∠BAD,
∴AD=BD.
(2)△ABC是等腰三角形.
理由:∵∠B=40°,∠BAC=70°,
∴∠C=180°﹣∠B﹣∠BAC=70°,
∴∠C=∠BAC,
∴BA=BC,
∴△ABC是等腰三角形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】下列事件为必然事件的是( )
A.任意买一张电影票,座位号是偶数
B.打开电视机,CCTV第一套节目正在播放天气预报
C.从一个只装有红色小球的不透明袋中,任意摸出一球是红球
D.经过某一有交通信号灯的路口,恰好遇到红灯
查看答案和解析>>
科目:初中数学 来源: 题型:
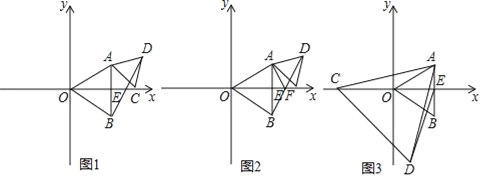
【题目】如图△AOB和△ACD是等边三角形,其中AB⊥x轴于E点.
(1)如图,若OC=5,求BD的长度;
(2)设BD交x轴于点F,求证:∠OFA=∠DFA;
(3)如图,若正△AOB的边长为4,点C为x轴上一动点,以AC为边在直线AC下方作正△ACD,连接ED,求ED的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB是⊙O的直径,点C是![]() 中点,∠COB=60°,过点C作CE⊥AD,交AD的延长线于点E
中点,∠COB=60°,过点C作CE⊥AD,交AD的延长线于点E

(1)求证:CE为⊙O的切线;
(2)判断四边形AOCD是否为菱形?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com