
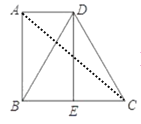
【题目】如图,四边形ABCD中,AD∥BC,∠ABC=90°,DB=DC,E是BC的中点,连接DE.
(1)求证:四边形ABED是矩形;
(2)连接AC,若∠ABD=30°,DC=2,求AC的长.

【答案】(1)见解析;(2)![]()
【解析】
(1)通过平行线的性质,证明∠BAD=90°,再通过等腰三角形的性质,可得∠DEB=90°,即可证明四边形ABED是矩形;
(2)先证明△DBC是等边三角形,可得BD=BC=DC=2,再根据含30度角的直角三角形的性质得出AB=![]() ,利用勾股定理即可得出AC的长.
,利用勾股定理即可得出AC的长.
(1)证明:∵AD∥BC,∠ABC=90°,
∴∠BAD=90°,
∵DB=DC,E是BC的中点,
∴∠DEB=90°,
∴四边形ABED是矩形;
(2)解:∵∠ABC=90°,∠ABD=30°,
∴∠DBE=60°,
∵DB=DC,
∴△DBC是等边三角形,
∴BD=BC=DC=2,
∵在Rt△BAD中,∠ABD=30°,BD=2,
∴AD=1,AB=![]() ,
,
∴在Rt△ABC中,AC=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】已知点A(x1,y1)、B(x2,y2)在二次函数y=x2+mx+n的图像上,当x1=1、x2=3时,y1=y2.
(1)若P(a,b1),Q(3,b2)是函数图象上的两点,b1>b2,则实数a的取值范围是( )
A.a<1 B.a>3 C.a<1或a>3 D.1<a<3
(2)若抛物线与x轴只有一个公共点,求二次函数的表达式.
(3)若对于任意实数x1、x2都有y1+y2≥2,则n的范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 纸片中,
纸片中,![]() ,学习小组进行如下操作:、如图2,沿
,学习小组进行如下操作:、如图2,沿![]() 折叠使点
折叠使点![]() 落在
落在![]() 延长线上的点
延长线上的点![]() 处,点
处,点![]() 是
是![]() .上一点,如图3,将图2展平后,再沿
.上一点,如图3,将图2展平后,再沿![]() 折叠使点
折叠使点![]() 落在点
落在点![]() 处,点
处,点![]() 分别在边
分别在边![]() 和
和![]() 上,将图3展平得到图4,连接
上,将图3展平得到图4,连接![]() ,请在图4中解决下列问题:
,请在图4中解决下列问题:
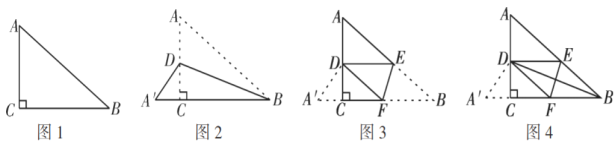
(1)判断四边形![]() 的形状, 并证明你的结论;
的形状, 并证明你的结论;
(2)若![]() ,求四边形
,求四边形![]() 的周长.
的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 、
、![]() ,顶点为M.
,顶点为M.
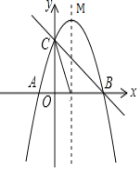
(1)求抛物线的解析式和点M的坐标;
(2)点E是抛物线段BC上的一个动点,设![]() 的面积为S,求出S的最大值,并求出此时点E的坐标;
的面积为S,求出S的最大值,并求出此时点E的坐标;
(3)在抛物线的对称轴上是否存在点P,使得以A、P、C为顶点的三角形是直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
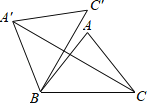
【题目】如图,在△ABC中,AB=AC=5,BC=6,将△ABC绕点B逆时针旋转60°得到△A'BC’,连接A'C,则A'C的长为( )
A. 6B. 4+2![]() C. 4+3
C. 4+3![]() D. 2+3
D. 2+3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解七年级学生的体重情况,随机抽取了七年级m名学生进行调查,将抽取学生的体重情况绘制如下不完整的频数分布表和扇形统计图.
组别 | 体重(千克) | 人数 |
A | 37.5≤x<42.5 | 10 |
B | 42.5≤x<47.5 | n |
C | 47.5≤x<52.5 | 40 |
D | 52.5≤x<57.5 | 20 |
E | 57.5≤x<62.5 | 10 |

请根据图表信息回答下列问题:
(1)填空:①m=_____,②n=_____,③在扇形统计图中,C组所在扇形的圆心角的度数等于_______度;
(2)若把每组中各个体重值用这组数据的中间值代替(例如:A组数据中间值为40千克),则被调查学生的平均体重是多少千克?
(3)如果该校七年级有1000名学生,请估算七年级体重低于47.5千克的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
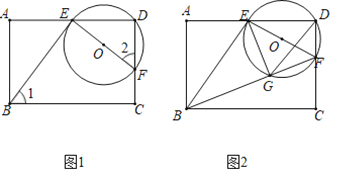
【题目】如图1,在矩形ABCD中,点E以lcm/s的速度从点A向点D运动,运动时间为t(s),连结BE,过点E作EF⊥BE,交CD于F,以EF为直径作⊙O.
(1)求证:∠1=∠2;
(2)如图2,连结BF,交⊙O于点G,并连结EG.已知AB=4,AD=6.
①用含t的代数式表示DF的长
②连结DG,若△EGD是以EG为腰的等腰三角形,求t的值;
(3)连结OC,当tan∠BFC=3时,恰有OC∥EG,请直接写出tan∠ABE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=BD,点E、F分别在BC、CD上,且BE=CF,连接BF、DE交于点M,延长ED到H使DH=BM,连接AM,AH,则以下四个结论:
①△BDF≌△DCE;②∠BMD=120°;③△AMH是等边三角形;④S四边形ABCD= ![]() AM2.
AM2.
其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com