
【题目】如图1,在![]() 纸片中,
纸片中,![]() ,学习小组进行如下操作:、如图2,沿
,学习小组进行如下操作:、如图2,沿![]() 折叠使点
折叠使点![]() 落在
落在![]() 延长线上的点
延长线上的点![]() 处,点
处,点![]() 是
是![]() .上一点,如图3,将图2展平后,再沿
.上一点,如图3,将图2展平后,再沿![]() 折叠使点
折叠使点![]() 落在点
落在点![]() 处,点
处,点![]() 分别在边
分别在边![]() 和
和![]() 上,将图3展平得到图4,连接
上,将图3展平得到图4,连接![]() ,请在图4中解决下列问题:
,请在图4中解决下列问题:
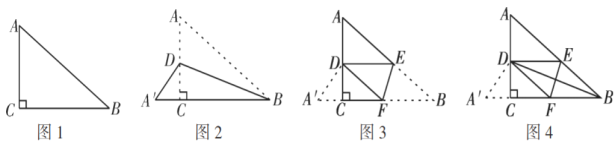
(1)判断四边形![]() 的形状, 并证明你的结论;
的形状, 并证明你的结论;
(2)若![]() ,求四边形
,求四边形![]() 的周长.
的周长.
【答案】(1)四边形![]() 是菱形,证明见解析;(2)
是菱形,证明见解析;(2)![]()
【解析】
(1)根据折叠的性质可知△DEF≌△BEF,DE=BE, ∠EDB=∠EBD, ∠BDF=∠DBF, ∠ABD=∠CBD,等量代换得∠EDB=∠EBD=∠BDF=∠DBF,得DE∥BF,DF∥BE,四边形DEBF是平行四边形,再加条件DE=BE,可得四边形DEBF是菱形;
(2)先由勾股定理求得AB长,再由平行线分线段成比例,求得BF的长,菱形周长即可求得.
解:![]() 四边形
四边形![]() 是菱形.
是菱形.
证明:![]() 沿
沿![]() 折叠,点
折叠,点![]() 落在
落在![]() 的延长线上的点
的延长线上的点![]() 处
处
![]() 是
是![]() 的平分线.
的平分线.
![]()
![]() 沿
沿![]() 折叠,点
折叠,点![]() 落在点
落在点![]() 处
处
![]() 是线段
是线段![]() 的垂直平分线.
的垂直平分线.
![]()
![]()
![]()
![]()
![]() 四边形
四边形![]() 是平行四边形
是平行四边形
![]()
![]() 四边形
四边形![]() 是菱形
是菱形
![]() 在
在![]() 中,
中,![]()
![]() 四边形
四边形![]() 是菱形
是菱形
![]()
![]()
![]()
即![]()
解得![]()
![]() 四边形
四边形![]() 的周长是
的周长是 ![]()


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边CD在正方形ECGF的边CE上,连接DG,过点A作AH∥DG,交BG于点H.连接HF,AF,其中AF交EC于点M.
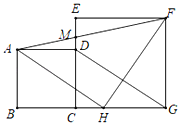
(1)求证:△AHF为等腰直角三角形.
(2)若AB=3,EC=5,求EM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,AB是直径,C为![]() 的中点,延长AD,BC交于点P,连结AC.
的中点,延长AD,BC交于点P,连结AC.
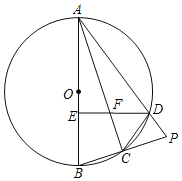
(1)求证:AB=AP;
(2)若AB=10,DP=2,
①求线段CP的长;
②过点D作DE⊥AB于点E,交AC于点F,求△ADF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 、
、![]() 两点的坐标分别为
两点的坐标分别为![]() ,
,![]() ,直线
,直线![]() 与反比例函数
与反比例函数![]() 的图象相交于点
的图象相交于点![]() 和点
和点![]() .
.

(1)求直线![]() 与反比例函数的解析式;
与反比例函数的解析式;
(2)求![]() 的度数;
的度数;
(3)将![]() 绕点
绕点![]() 顺时针方向旋转
顺时针方向旋转![]() 角(
角(![]() 为锐角),得到
为锐角),得到![]() ,当
,当![]() 为多少度时
为多少度时![]() ,并求此时线段
,并求此时线段![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接2022年冬奥会,鼓励更多的学生参与到志愿服务中来,甲、乙两所学校组织了志愿服务团队选拔活动.为了了解两所学校学生的整体情况,从两校进入综合素质展示环节的学生中分别随机抽取了50名学生的综合素质展示成绩(百分制),并对数据(成绩)进行整理、描述和分析.下面给出了部分信息.
a.甲学校学生成绩的频数分布直方图如图:

b.甲学校学生成绩在80~90这一组的是:
80 | 80 | 81 | 81 | 82 | 82 | 83 | 83 |
85 | 86 | 86 | 87 | 88 | 88 | 89 | 89 |
c.乙学校学生成绩的平均数、中位数、众数、优秀率(85分及以上为优秀)如下:
平均数 | 中位数 | 众数 | 优秀率 |
85 | 84 | 78 | 46% |
根据以上信息,回答下列问题:
(1)甲学校学生成绩的中位数为 分;
(2)甲学校学生A、乙学校学生B的综合素质展示成绩同为83分,这两人在本校学生中的综合素质展示排名更靠前的是 (填“A”或“B”);
(3)根据上述信息,推断哪所学校综合素质展示的水平更高,并至少从两个不同的角度说明推断的合理性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中学生骑电动车上学的现象越来越受到社会的关注.为此某媒体记者小李随机调查了城区若干名中学生家长对这种现象的态度(态度分为:A:无所谓;B:反对;C:赞成)并将调査结果绘制成图①和图②的统计图(不完整)请根据图中提供的信息,解答下列问题:
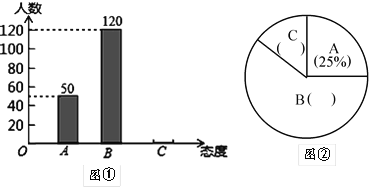
(1)此次抽样调査中.共调査了______名中学生家长;
(2)将图形①、②补充完整;
(3)根据抽样调查结果.请你估计我市城区80000名中学生家长中有多少名家长持反对态度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AD∥BC,∠ABC=90°,DB=DC,E是BC的中点,连接DE.
(1)求证:四边形ABED是矩形;
(2)连接AC,若∠ABD=30°,DC=2,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知抛物线y=x2-2mx-3m
(1)当m=1时,
①抛物线的对称轴为直线______,
②抛物线上一点P到x轴的距离为4,求点P的坐标
③当n≤x≤![]() 时,函数值y的取值范围是-
时,函数值y的取值范围是-![]() ≤y≤2-n,求n的值
≤y≤2-n,求n的值
(2)设抛物线y=x2-2mx-3m在2m-1≤x≤2m+1上最低点的纵坐标为y0,直接写出y0与m之间的函数关系式及m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com