
����Ŀ����ͼ��������y=��x2+bx+c��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����A������Ϊ����1��0������y�ύ�ڵ�C��0��3������ֱ��BC������P��x�����˶�������P��PM��x�ᣬ���������ڵ�M����ֱ��BC�ڵ�N�����P�ĺ�����Ϊm��
�������������ߵĽ���ʽ��ֱ��BC�Ľ���ʽ��
����������P���߶�OB���˶�ʱ�����߶�MN�����ֵ��
����������C��O��M��NΪ������ı�����ƽ���ı���ʱ��ֱ��д��m��ֵ��

���𰸡���1��y=��x2+2x+3��y=��x+3����2��![]() ����3��
����3��![]() ��
��![]()
�������������������1����A��C������������ߵĽ���ʽ���з���������b��c��ֵ����y=0���ⷽ�̿ɵ�B�����꣬���ô���ϵ������ֱ��BC�Ľ���ʽ��
��2�����ݽ���ʽ�ֱ��ʾM��N��������꣬��������IJ����MN�ij����䷽������ֵ���ɣ�
��3�������������������P���߶�OB��ʱ������MN=��m2+3m��������P�����߶�OB��ʱ������MN=��m+3������m2+2m+3��=m2��3m������MN=3�з��̽�����ɣ�
����������⣺��1���������߹�A��C���㣬�����������߽���ʽ�ɵã� ![]() ����ã�
����ã� ![]() ���������߽���ʽΪy=��x2+2x+3����y=0�ɵã���x2+2x+3=0����x1=��1��x2=3����B����A���Ҳ࣬��B������Ϊ��3��0������ֱ��BC����ʽΪy=kx+s����B��C�������ɵ���
���������߽���ʽΪy=��x2+2x+3����y=0�ɵã���x2+2x+3=0����x1=��1��x2=3����B����A���Ҳ࣬��B������Ϊ��3��0������ֱ��BC����ʽΪy=kx+s����B��C�������ɵ��� ![]() �������
������� ![]() ����ֱ��BC����ʽΪy=��x+3��
����ֱ��BC����ʽΪy=��x+3��
��2����PM��x�ᣬ��P�ĺ�����Ϊm����M��m����m2+2m+3����N��m����m+3������P���߶�OB���˶�����M����N���Ϸ�����MN=��m2+2m+3������m+3��=��m2+3m=����m��![]() ��2+
��2+![]() ������m=
������m=![]() ʱ��MN�����ֵ��MN�����ֵΪ
ʱ��MN�����ֵ��MN�����ֵΪ![]() ��
��
��3����PM��x�ᣬ��MN��OC������C��O��M��NΪ������ı�����ƽ���ı���ʱ������OC=MN������P���߶�OB��ʱ������MN=��m2+3m���ੁm2+3m=3���˷�����ʵ����������P�����߶�OB��ʱ������MN=��m+3������m2+2m+3��=m2��3m����m2��3m=3�����m=![]() ��m=
��m=![]() ��
��
���Ͽ�֪����C��O��M��NΪ������ı�����ƽ���ı���ʱ��m��ֵΪ![]() ��
��![]() ��
��


 �ŵ������ϵ�д�
�ŵ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ABCD������AB��AD�ij��ǹ���x�ķ���x2��mx��![]() ��
��![]() ��0������ʵ������
��0������ʵ������
(1)��mΪ��ֵʱ���ı���ABCD�����Σ������ʱ���εı߳���
(2)��AB�ij�Ϊ2����ô��ABCD���ܳ��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����ϣ�
��![]() ��
��![]() ��
��![]() �����������ж��θ�ʽ�Ĵ���ʽ��ˣ��������ж��θ�ʽ�����dz�����������ʽ��Ϊ��������ʽ.����
�����������ж��θ�ʽ�Ĵ���ʽ��ˣ��������ж��θ�ʽ�����dz�����������ʽ��Ϊ��������ʽ.����![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �ȶ��ǻ�Ϊ��������ʽ.
�ȶ��ǻ�Ϊ��������ʽ.
�ڽ��ж��θ�ʽ����ʱ��������������ʽ�����Ի�ȥ��ĸ�еĸ��š�
���磺![]() ��
��
����������⣺
��1��![]() �� ��Ϊ��������ʽ����
�� ��Ϊ��������ʽ����![]() ��ĸ��������
��ĸ��������
��2�����㣺![]()
��3���۲�����ı��ι��ɲ�������⣺
��![]() ��
��![]() ��
��![]() ��
��![]() ������
������![]() ���������������
���������������![]()
�ڼ��㣺![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����۴��Ҫ�����̻����죬��֪����A������3�ã�B������4�ã���Ҫ370Ԫ������A������5�ã�B������2�ã���Ҫ430Ԫ
��1������A��B��������ÿ�ø������Ԫ��
��2�����蹺�����������繲100�ã�Ҫ����������������ʽ���5860Ԫ��������ܹ�����ٿ�A�����磿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��E��F�ֱ���ABCD��AD��BC���ϵĵ㣬��AE=CF��

��1����֤����ABE�ա�CDF��
��2����M��N�ֱ���BE��DF���е㣬����MF��EN�����ж��ı���MFNE���������ı��Σ���֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���Բμ�2019���п���300�����б�ҵ��������һ�������������飬���Ƴ�Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ.

�����ͼ����Ϣ�ش��������⣺
(1)![]() __________��
__________��![]() __________��
__________��
(2)��Ƶ���ֲ�ֱ��ͼ����������
(3)��������4.9����(��4.9)��Ϊ��������������Ϣ����ȫ�����б�ҵ��������������ѧ���ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
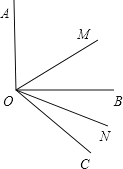
����Ŀ��(1)��ͼ��ʾ����֪��AOB��90������BOC��30����OMƽ�֡�AOC��ONƽ�֡�BOC�����MON�Ķ�����
(2)���(1)�С�AOB�����������������䣬���MON�Ķ�����
(3)���(1)�С�BOC����(��Ϊ���)�������������������MON�Ķ�����
(4)��(1)(2)(3)�Ľ�������ܿ���ʲô���ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����110��������ͬ��Сľ��������ͼ��ʾ�ķ�ʽ,�����������λ�������,Ҫ�����ڵ�ͼ��ֻ��һ��������.
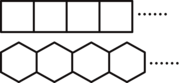
(1)С��������![]() ��Сľ���ڳ���
��Сľ���ڳ���![]() ��С������,�����õ�ʽ��ʾ
��С������,�����õ�ʽ��ʾ![]() ֮��Ĺ�ϵ�� ��
֮��Ĺ�ϵ�� ��
(2)С����ʣ�µ�Сľ���ڳ���һЩ������,��û��ľ��ʣ��.��֪���ڳ��������α������ζ�4��,��������ڷŵ������κ������θ����ٸ�?
(3)С��������50��Сľ��,�ڳ���![]() ��,��
��,��![]() ��С������.����ÿ�����ٺ���1��С������,ÿ�ź��е�С�����εĸ������Բ�ͬ.�����õ�ʽ��ʾ
��С������.����ÿ�����ٺ���1��С������,ÿ�ź��е�С�����εĸ������Բ�ͬ.�����õ�ʽ��ʾ![]() ֮��Ĺ�ϵ,��д������
֮��Ĺ�ϵ,��д������![]() ���ܵ�ȡֵ.
���ܵ�ȡֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������y=ax+b��y=bx+a��ͼ����ͬһ����ϵ�ڵĴ���λ����ȷ���ǣ�������
A.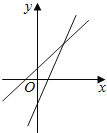 B.
B.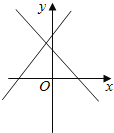
C.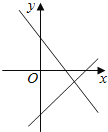 D.
D.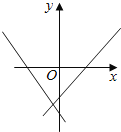
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com