
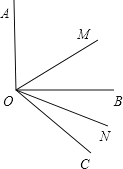
【题目】(1)如图所示,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数;
(2)如果(1)中∠AOB=α,其他条件不变,求∠MON的度数;
(3)如果(1)中∠BOC=β(β为锐角),其他条件不变,求∠MON的度数;
(4)从(1)(2)(3)的结果中你能看出什么规律?
【答案】(1)45°(2)![]() (3)45°(4)∠MON的大小总等于∠AOB的一半,与锐角∠BOC的大小无关.
(3)45°(4)∠MON的大小总等于∠AOB的一半,与锐角∠BOC的大小无关.
【解析】(1)先求出∠MOC的度数:(90+30)÷2=60°,∠CON的度数是:30÷2=15°,然后用∠MOC的度数减去∠CON的度数即可得出∠MON的度数.
(2)根据问题(1)的解题思路把∠AOB的度数用字母a代替即可.
(3)根据问题(1)的解题思路把∠BOC的度数用字母![]() 代替即可.
代替即可.
(4)根据(1)(2)(3)的得数可知:∠MON的度数是始终是∠AOB的度数的一半》
解:(1)因为OM平分∠AOC,
所以∠MOC=![]() ∠AOC.
∠AOC.
又因为ON平分∠BOC,
所以∠NOC=![]() ∠BOC.
∠BOC.
所以∠MON=∠MOC-∠NOC=![]() ∠AOC-
∠AOC-![]() ∠BOC=
∠BOC=![]() (∠AOC-∠BOC)=
(∠AOC-∠BOC)=![]() ∠AOB.
∠AOB.
又因为∠AOB=90°,所以∠MON=45°.
(2)当∠AOB=α,其他条件不变时,∠MON=![]() .
.
(3)当∠BOC=β,其他条件不变时,∠MON=45°.
(4)分析(1)(2)(3)的结果和(1)的解答过程可知:∠MON的大小总等于∠AOB的一半,与锐角∠BOC的大小无关.
“点睛”本题考查了组合角中某个角的度数的求解,根据是明确各角之间的联系.


科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=120°,以CA为边在∠ACB的另一侧作∠ACM=∠ACB,点D为射线CM上任意一点,在射线CM上载取CE=BD,连接AD、AE.
(1)如图1,当点D落在线段BC的延长线上时,求证:△ABD≌△ACE;
(2)在(1)的条件下,求出∠ADE的度数;
(3)如图2,当点D落在线段BC(不含端点)上时,作AH⊥BC,垂足为H,作AG⊥EC,垂足为G,连接HG,判断△GHC的形状,并说明现由.

查看答案和解析>>
科目:初中数学 来源: 题型:
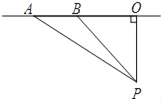
【题目】超速行驶是引发交通事故的主要原因.上周末,小明和三位同学尝试用自己所学的知识检测车速,如图,观测点设在到县城城南大道的距离为100米的点P处.这时,一辆出租车由西向东匀速行驶,测得此车从A处行驶到B处所用的时间为4秒,且∠APO=60°,∠BPO=45°.
(1)求A、B之间的路程;
(2)请判断此出租车是否超过了城南大道每小时60千米的限制速度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A、B两点(点A在点B的左侧),点A的坐标为(﹣1,0),与y轴交于点C(0,3),作直线BC.动点P在x轴上运动,过点P作PM⊥x轴,交抛物线于点M,交直线BC于点N,设点P的横坐标为m.
(Ⅰ)求抛物线的解析式和直线BC的解析式;
(Ⅱ)当点P在线段OB上运动时,求线段MN的最大值;
(Ⅲ)当以C、O、M、N为顶点的四边形是平行四边形时,直接写出m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
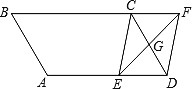
【题目】如图,在平行四边形ABCD中,AB=4cm,BC=6cm,∠B=60°,G是CD的中点,E是边AD上的动点(E不与A、D重合),且点E由A向D运动,速度为1cm/s,EG的延长线与BC的延长线交于点F,连接CE、DF,设点E的运动时间为![]()
(1)求证:无论![]() 为何值,四边形CEDF都是平行四边形;
为何值,四边形CEDF都是平行四边形;
(2)①当![]() s时,CE⊥AD;
s时,CE⊥AD;
②当![]() 时,平行四边形CEDF的两条邻边相等.
时,平行四边形CEDF的两条邻边相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在直角坐标系中,已知A(0,a),B(b,0)C(3,c)三点,若a,b,c满足关系式:|a﹣2|+(b﹣3)2+![]() =0.
=0.
(1)求a,b,c的值.
(2)求四边形AOBC的面积.
(3)是否存在点P(x,﹣![]() x),使△AOP的面积为四边形AOBC的面积的两倍?若存在,求出点P的坐标,若不存在,请说明理由.
x),使△AOP的面积为四边形AOBC的面积的两倍?若存在,求出点P的坐标,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小静带着100元钱去文具店购买日记本,到文具店她发现该文具店对日记本正在开展¨满100减30”的促销活动.即购买日记本的费用达到或超过100元就可以少付30元.小静通过计算发现,在该店买6个日记本的费用比买5个日记本的费用低.请你计算一个日记本的价格可以是__________元.(设日记本的价格为正整数,请写出所有可能的结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①点O与O′的距离为4;②∠AOB=150°;③![]() .其中正确的结论是( )
.其中正确的结论是( )

A. ①B. ①②C. ②③D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】湘潭市继2017年成功创建全国文明城市之后,又准备争创全国卫生城市.某小区积极响应,决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买2个温馨提示牌和3个垃圾箱共需550元,且垃圾箱的单价是温馨提示牌单价的3倍.
(1)求温馨提示牌和垃圾箱的单价各是多少元?
(2)该小区至少需要安放48个垃圾箱,如果购买温馨提示牌和垃圾箱共100个,且费用不超过10000元,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com