
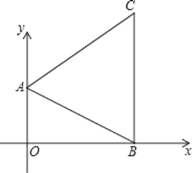
【题目】如图在直角坐标系中,已知A(0,a),B(b,0)C(3,c)三点,若a,b,c满足关系式:|a﹣2|+(b﹣3)2+![]() =0.
=0.
(1)求a,b,c的值.
(2)求四边形AOBC的面积.
(3)是否存在点P(x,﹣![]() x),使△AOP的面积为四边形AOBC的面积的两倍?若存在,求出点P的坐标,若不存在,请说明理由.
x),使△AOP的面积为四边形AOBC的面积的两倍?若存在,求出点P的坐标,若不存在,请说明理由.

【答案】(1)a=2,b=3,c=4;(2)9;(3)存在点P(18,﹣9)或(﹣18,9),使△AOP的面积为四边形AOBC的面积的两倍.
【解析】
(1)根据“几个非负数相加和为0,则每一个非负数的值均为0”解出a,b,c的值;
(2)由点A、O、B、C的坐标可得四边形AOBC为直角梯形,根据直角梯形的面积公式计算即可;
(3)设存在点P(x,﹣![]() x),使△AOP的面积为四边形AOBC的面积的两倍.根据面积列出方程
x),使△AOP的面积为四边形AOBC的面积的两倍.根据面积列出方程![]() ×2×|x|=|x|=2×9,解方程即可.
×2×|x|=|x|=2×9,解方程即可.
解:(1)∵|a﹣2|+(b﹣3)2+![]() =0,
=0,
∴a﹣2=0,b﹣3=0,c﹣4=0,
∴a=2,b=3,c=4;
(2)∵A(0,2),O(0,0),B(3,0),C(3,4);
∴四边形AOBC为直角梯形,且OA=2,BC=4,OB=3,
∴四边形AOBC的面积=![]() ×(OA+BC)×OB=
×(OA+BC)×OB=![]() ×(2+4)×3=9;
×(2+4)×3=9;
(3)设存在点P(x,﹣![]() x),使△AOP的面积为四边形AOBC的面积的两倍.
x),使△AOP的面积为四边形AOBC的面积的两倍.
∵△AOP的面积=![]() ×2×|x|=|x|,
×2×|x|=|x|,
∴|x|=2×9,
∴x=±18
∴存在点P(18,﹣9)或(﹣18,9),
使△AOP的面积为四边形AOBC的面积的两倍.
故答案为:(1)a=2,b=3,c=4;(2)9;(3)存在点P(18,﹣9)或(﹣18,9),使△AOP的面积为四边形AOBC的面积的两倍.


科目:初中数学 来源: 题型:
【题目】如图,已知直线y=﹣![]() x+3与x轴、y轴分别相交于点A、B,再将△A0B沿直钱CD折叠,使点A与点B重合.折痕CD与x轴交于点C,与AB交于点D.
x+3与x轴、y轴分别相交于点A、B,再将△A0B沿直钱CD折叠,使点A与点B重合.折痕CD与x轴交于点C,与AB交于点D.
(1)点A的坐标为 ;点B的坐标为 ;
(2)求OC的长度,并求出此时直线BC的表达式;
(3)直线BC上是否存在一点M,使得△ABM的面积与△ABO的面积相等?若存在,请直接写出点M的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】景观大道要进行绿化改造,已知购买A种树苗3棵,B种树苗4棵,需要370元;购买A种树苗5棵,B种树苗2棵,需要430元
(1)求购买A,B两种树苗每棵各需多少元?
(2)现需购买这两种树苗共100棵,要求购买这两种树苗的资金不超过5860元,求最多能购买多少棵A种树苗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区对参加2019年中考的300名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图.

请根据图表信息回答下列问题:
(1)![]() __________,
__________,![]() __________;
__________;
(2)将频数分布直方图补充完整;
(3)若视力在4.9以上(含4.9)均为正常,据以上信息估计全区初中毕业生中视力正常的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
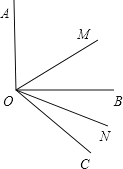
【题目】(1)如图所示,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数;
(2)如果(1)中∠AOB=α,其他条件不变,求∠MON的度数;
(3)如果(1)中∠BOC=β(β为锐角),其他条件不变,求∠MON的度数;
(4)从(1)(2)(3)的结果中你能看出什么规律?
查看答案和解析>>
科目:初中数学 来源: 题型:
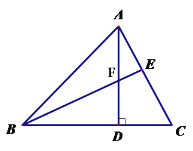
【题目】如图,AD为△ABC的高,E为AC上一点,BE交AD于F,且有BF=AC, FD=CD。求证:(1) Rt△BDF≌Rt△ADC (2) BE⊥AC
查看答案和解析>>
科目:初中数学 来源: 题型:
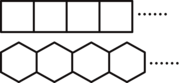
【题目】小红用110根长短相同的小木棍按照如图所示的方式,连续摆正方形或六边形,要求相邻的图形只有一条公共边.
(1)小红首先用![]() 根小木棍摆出了
根小木棍摆出了![]() 个小正方形,请你用等式表示
个小正方形,请你用等式表示![]() 之间的关系: ;
之间的关系: ;
(2)小红用剩下的小木棍摆出了一些六边形,且没有木棍剩余.已知他摆出的正方形比六边形多4个,请你求出摆放的正方形和六边形各多少个?
(3)小红重新用50根小木棍,摆出了![]() 排,共
排,共![]() 个小正方形.其中每排至少含有1个小正方形,每排含有的小正方形的个数可以不同.请你用等式表示
个小正方形.其中每排至少含有1个小正方形,每排含有的小正方形的个数可以不同.请你用等式表示![]() 之间的关系,并写出所有
之间的关系,并写出所有![]() 可能的取值.
可能的取值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图中小方格都是边长为1的正方形,△ABC与△A′B′C′是关于点G为位似中心的位似图形,它们的顶点都在小正方形顶点上.
(1)画出位似中心点G;
(2)若点A、B在平面直角坐标系中的坐标分别为(﹣6,0),(-3,2),点P(m,n)是线段AC上任意一点,则点P在△A′B′C′上的对应点P′的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
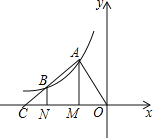
【题目】如图,点A、B在反比例函数y=![]() 的图象上,过点A、B作x轴的垂线,垂足分别是M、N,射线AB交x轴于点C,若OM=MN=NC,四边形AMNB的面积是3,则k的值为( )
的图象上,过点A、B作x轴的垂线,垂足分别是M、N,射线AB交x轴于点C,若OM=MN=NC,四边形AMNB的面积是3,则k的值为( )
A.2 B.4 C.﹣2 D.﹣4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com