
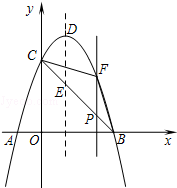
 如图,抛物线y=-x2+2x+3与x轴相交于A、B两点(点A在点B的左侧),与y轴交于点C,顶点为D.
如图,抛物线y=-x2+2x+3与x轴相交于A、B两点(点A在点B的左侧),与y轴交于点C,顶点为D.分析 (1)对于抛物线解析式,令x=0求出y的值,确定出OC的值,得出C的坐标,令y=0求出x的值,确定出B的坐标,进而得出抛物线对称轴;
(2)①设直线BC的解析式为y=kx+b,将B与C坐标代入求出k与b的值,即可确定出直线BC解析式;由二次函数解析式易得抛物线顶点D的坐标,结合一次函数图象上点坐标特征可以推知点E坐标,由点的坐标与图形是性质求得DE、PF的长度;然后由DE∥FP,欲使四边形PEDF为平行四边形,只需DE=PF,列出关于m的方程,求出方程的解得到m的值,检验即可.
②由三角形的面积公式列出S与m的函数关系式.
(3)需要分类讨论:①以BH为边,②以BH为对角线.确定平行四边形后,可直接利用平行四边形的性质求出H点的坐标.
解答  解:(1)如图,∵在y=-x2+2x+3中,当x=0时,y=3,
解:(1)如图,∵在y=-x2+2x+3中,当x=0时,y=3,
∴C(0,3),
当y=0时,-x2+2x+3=0,
解得:x1=-1,x2=3,
∵点A在点B的左侧,
∴B(3,0),
抛物线的对称轴是:x=-$\frac{b}{2a}$=1;
(2)①设直线BC的函数关系式为:y=kx+b(k≠0).
把B(3,0),C(0,3)分别代入得:$\left\{\begin{array}{l}{3k+b=0}\\{b=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=3}\end{array}\right.$,
∴直线BC的函数关系式为:y=-x+3;
由y=-x2+2x+3=-(x-1)2+4得到:D(1,4),
当x=1时,y=-1+3=2,即E(1,2).
当x=m时,y=-m+3,则P(m,-m+3).
当x=m时,y=-m2+2m+3,即F(m,-m2+2m+3),
∴DE=4-2=2,PF=-m2+2m+3-(-m+3)=-m2+3m,
∵PF∥DE,
∴当PF=ED时,四边形PEDF为平行四边形,
由-m2+3m=2,解得:m1=2,m2=1(不合题意,舍去).
则当m=2时,四边形PEDF为平行四边形.
②S=$\frac{1}{2}$PF•OB=$\frac{1}{2}$×(-m2+3m)×3=-$\frac{3}{2}$m2+$\frac{9}{2}$m,即S=-$\frac{3}{2}$m2+$\frac{9}{2}$m(0≤m≤3);
(3)若以B、C、G、H为顶点的四边形是平行四边形,
①BH为四边形的边,则CG∥BH,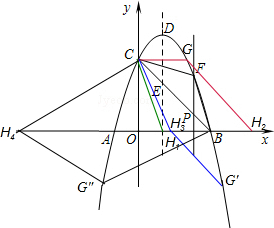
故点G和点C关于直线x=1对称,
∴G(2,3)且CG=2,
此时BH=2,
∴H1(1,0)或H2(5,0);
②BH为对角线,则此时G的纵坐标为-3,
∴-x2+2x+3=-3,可得x=1±$\sqrt{7}$,
故G′(1+$\sqrt{7}$,-3),G″(1-$\sqrt{7}$,-3),
B、H关于点($\frac{1+\sqrt{7}}{2}$,0)或($\frac{1-\sqrt{7}}{2}$,0)对称,
所以H3($\sqrt{7}$-2,0),H4(-$\sqrt{7}$-2,0),
综上,点H坐标为H1(1,0)或H2(5,0)或H3($\sqrt{7}$-2,0)或H4(-$\sqrt{7}$-2,0).
点评 此题考查了二次函数解析式的确定、轴对称的性质以及平行四边形的判定和性质;要特别注意的是(3)题中,由于没有明确BH是平行四边形的边还是对角线,所以一定要分类讨论,以免漏解.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案科目:初中数学 来源: 题型:选择题
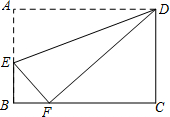 如图,长方形ABCD中,点E 在边AB上,将长方形ABCD沿直线DE折叠,点A恰好落在边BC上的点F处,若AD=5,DC=3,则BF的长是( )
如图,长方形ABCD中,点E 在边AB上,将长方形ABCD沿直线DE折叠,点A恰好落在边BC上的点F处,若AD=5,DC=3,则BF的长是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源:2016-2017学年浙江省瑞安市五校联考八年级下学期第一次月考数学试卷(解析版) 题型:单选题
下列式子中,属于最简二次根式的是( )
A. 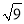 B.
B. 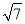 C.
C. 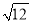 D.
D. 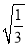
查看答案和解析>>
科目:初中数学 来源:2017届江苏省盐都市九年级下学期第一次学情调研数学试卷(解析版) 题型:填空题
某药品原价每盒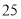 元,为了响应国家解决老百姓看病贵的号召,经过连续两次降价,现在售价每盒
元,为了响应国家解决老百姓看病贵的号召,经过连续两次降价,现在售价每盒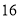 元,则该药品平均每次降价的百分率是_______.
元,则该药品平均每次降价的百分率是_______.
查看答案和解析>>
科目:初中数学 来源:2017届江苏省盐都市九年级下学期第一次学情调研数学试卷(解析版) 题型:单选题
左图是由八个相同小正方体组合而成的几何体,则其俯视图是( )
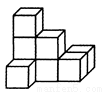
A. 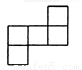 B.
B. 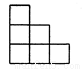 C.
C. 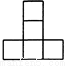 D.
D. 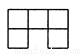
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
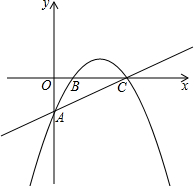 如图:在平面直角坐标系中,直线$y=\frac{1}{2}x-2$分别交x、y轴于C、A,抛物线y=-$\frac{1}{2}$x2+bx+c经过A、C两点,交x轴于另外一点B.
如图:在平面直角坐标系中,直线$y=\frac{1}{2}x-2$分别交x、y轴于C、A,抛物线y=-$\frac{1}{2}$x2+bx+c经过A、C两点,交x轴于另外一点B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
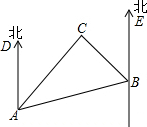 海面上的A,B,C三艘船的平面图如图所示,C船在A船的北偏东55°方向,B船在A船的北偏东85°方向,C船在B船的北偏西25°方向.
海面上的A,B,C三艘船的平面图如图所示,C船在A船的北偏东55°方向,B船在A船的北偏东85°方向,C船在B船的北偏西25°方向.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com