
【题目】我们已经学习了一元二次方程的多种解法:如因式分解法,开平方法,配方法和公式法,还可以运用十字相乘法,请从以下一元二次方程中任选一个,并选择你认为适当的方法解这个方程.
①x2﹣4x﹣1=0
②x(2x+1)=8x﹣3
③x2+3x+1=0
④x2﹣9=4(x﹣3)
我选择第个方程.
【答案】①或②或③或④
【解析】解:我选第①个方程,解法如下:
x2﹣4x﹣1=0,
这里a=1,b=﹣4,c=﹣1,
∵△=16+4=20,
∴x= ![]() =2±
=2± ![]() ,
,
则x1=2+ ![]() ,x2=2﹣
,x2=2﹣ ![]() ;
;
我选第②个方程,解法如下:
x(2x+1)=8x﹣3,
整理得:2x2﹣7x+3=0,
分解因式得:(2x﹣1)(x﹣3)=0,
可得2x﹣1=0或x﹣3=0,
解得:x1= ![]() ,x2=3;
,x2=3;
我选第③个方程,解法如下:
x2+3x+1=0,
这里a=1,b=3,c=1,
∵△=9﹣4=5,
∴x= ![]() ,
,
则x1= ![]() ,x2=
,x2= ![]() ;
;
我选第④个方程,解法如下:
x2﹣9=4(x﹣3),
变形得:(x+3)(x﹣3)﹣4(x﹣3)=0,
分解因式得:(x﹣3)(x+3﹣4)=0,
可得x﹣3=0或x﹣1=0,
解得:x1=1,x2=3
【考点精析】认真审题,首先需要了解配方法(左未右已先分离,二系化“1”是其次.一系折半再平方,两边同加没问题.左边分解右合并,直接开方去解题),还要掌握公式法(要用公式解方程,首先化成一般式.调整系数随其后,使其成为最简比.确定参数abc,计算方程判别式.判别式值与零比,有无实根便得知.有实根可套公式,没有实根要告之)的相关知识才是答题的关键.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,BD、BE分别是高和角平分线,点F在CA的延长线上,FH⊥BE,交BD于点G,交BC于点H.下列结论:①∠DBE=∠F;②2∠BEF=∠BAF+∠C;③∠F=∠BAC-∠C;④∠BGH=∠ABE+∠C.其中正确的有( )
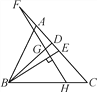
A. ①②③ B. ①②④ C. ②③④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD中,AB=4cm,BC=3cm,E为CD的中点.动点P从A点出发,以每秒1cm的速度沿A﹣B﹣C﹣E运动,最终到达点E.若点P运动的时间为x秒,则当x=__时,△APE的面积等于5.
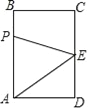
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班数学兴趣小组8名同学的毕业升学体育测试成绩依次为:30,29,28,27,28,29,30,28,这组数据的众数是( )
A. 27 B. 28 C. 29 D. 30
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:一组数据x1 , x2 , x3 , x4 , x5的平均数是2,方差是 ![]() ,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数和方差分别是( )
,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数和方差分别是( )
A.2, ![]()
B.2,1
C.4, ![]()
D.4,3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com