
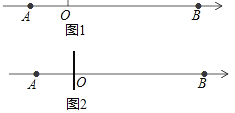
����Ŀ����ͼ1����������A���ʾ��a��B���ʾ��b��AB��ʾA���B��֮��ľ��룬��a��b����|a+4|+|b+3a|��0��
��1����A��B����֮��ľ��룻
��2�����������ϴ���һ��C����AC+BC��19����C���ʾ������
��3����ͼ2������ԭ��O����һ���壬һС��״ӵ�A����2����λ/����ٶ������˶����������һ��С���Ҵӵ�B����3����λ/����ٶ�Ҳ�����˶������������������Ĵ�С���ɿ���һ�㣩������4����λ/����ٶ����෴�����˶���������˶���ʱ��Ϊt���룩��
�ٷֱ��ʾ�ס�����С��ԭ��ľ��루�ú�t��ʽ�ӱ�ʾ����
����ס�����С��ԭ��ľ������ʱ����������λ�ö�Ӧ������
���𰸡���1��A��B����֮��ľ�����16����2����C�������߶�AB�ϣ���C��������߶�BA���ӳ����ϻ��߶�AB���ӳ����ϣ���AC+BC��19��C��ʾ����Ϊ![]() ��
��![]() ����3��������ԭ��ľ���Ϊ��12��3��t��2����������ԭ��ľ���Ϊ��2t+4���ڼס�����С��ԭ��ľ������ʱ����������λ�ö�Ӧ����Ϊ��
����3��������ԭ��ľ���Ϊ��12��3��t��2����������ԭ��ľ���Ϊ��2t+4���ڼס�����С��ԭ��ľ������ʱ����������λ�ö�Ӧ����Ϊ��![]() ��48��
��48��
��������
��1���ȸ��ݷǸ������������a��b��ֵ���ٸ��������ľ��빫ʽ�������A��B����֮��ľ��룻
��2����C�����߶�BA�ӳ����Ϻ��߶�AB�ӳ���������������ۼ�����⣻
��3���ټ���ԭ��ľ��룽�����˶���·��+OA�ij�������ԭ��ľ���������������������ӵ�B����ʼ�����˶���һֱ��ԭ��O����ʱOB�ij��ȩ������˶���·�̼�Ϊ����ԭ��ľ��룻���������ԭ��O����ʼ�����˶�����ʱ�����˶���·�̩�OB�ij��ȼ�Ϊ����ԭ��ľ��룻
�ڰ��ٷ�����������ݼס�����С��ԭ��ľ�������г�����t�ķ��̣��ⷽ�̼��ɣ�
�⣺��1����|a+4|+|b+3b|��0��
��a+4��0��b+3a��0��
��a����4��b����3a��12��
��AB��|b��a|��|12������4��|��16
��A��B����֮��ľ�����16��
��2���������ϵ�C��ʾ����Ϊc
��AC��|c��a|��|c+4|��BC��|c��b|��|c��12|
��AC+BC��19
��|c+4|+|c��12|��19
��AB��16��19
���C�������߶�AB�ϣ���C��������߶�BA���ӳ����ϻ��߶�AB���ӳ����ϣ�
�ٵ�C�����߶�BA�ӳ�����ʱ������c�ܩ�4��
��|c+4|������c+4����|c��12|������c��12��
�ੁ��c+4������c��12����19
��ã�c��![]()
�ڵ�C�����߶�AB���ӳ�����ʱ������c��12��
��|c+4|��c+4��|c��12|��c��12
��c+4+c��12��19
��ã�c��![]()
������˵����AC+BC��19��C��ʾ����Ϊ![]() ��
��![]() ��
��
��3���١����˶���·��Ϊ��2t��2t��OA��4
�������ԭ��ľ���Ϊ��2t+4
����ԭ��ľ�������������
����0��t��4ʱ������ӵ�B����ʼ�����˶���һֱ��ԭ��O��
��OB��12�������˶���·��Ϊ��3t��3t��
������ԭ��ľ���Ϊ��12��3��t��2����
����t��4ʱ�������ԭ��O����ʼһֱ�����˶���
������ԭ��ľ���Ϊ��3��t��2����12��
�ڵ�0��t��4ʱ����2t+4��12��3��t��2����
��ã�t��![]()
�ੁ4��2t��![]()
��t��4ʱ����2t+4��3��t��2����12��
��ã�t��22
�ੁ4��2t����48
�����������ס�����С��ԭ��ľ������ʱ����������λ�ö�Ӧ����Ϊ��![]() ��48��
��48��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
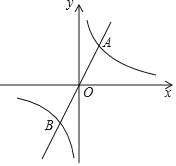
����Ŀ����ͼ����֪����������y=2x�뷴��������y=![]() ��k��0����ͼ����A��B���㣬�ҵ�A�ĺ�����Ϊ4��
��k��0����ͼ����A��B���㣬�ҵ�A�ĺ�����Ϊ4��
��1����k��ֵ��
��2������ͼ��ֱ��д������������ֵС�ڷ���������ֵʱx��ȡֵ��Χ��
��3����ԭ��O����һ��ֱ��l��˫����y=![]() ��k��0����P��Q���㣨P���ڵ�һ���ޣ������ɵ�A��P��B��QΪ������ɵ��ı������Ϊ224�����P�����꣮
��k��0����P��Q���㣨P���ڵ�һ���ޣ������ɵ�A��P��B��QΪ������ɵ��ı������Ϊ224�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ����С��Ϊ�˽�ͬѧ�Ƕ�ѧУ�������ܲ������ϲ���̶�,��ȡ����ѧ�����е���.�������ÿ��ѧ����A(�dz�ϲ��)��B(�Ƚ�ϲ��)��C(һ��)��D(��ϲ��)�ĸ��ȼ��Ի����.ͼ1��ͼ2�Ǹ�С��ɼ����ݺ���Ƶ�����ͳ��ͼ.��ȷ������ͳ��ͼ����ȷ�ģ�������ͳ��ͼ����һ�������Ҳ�������.�������ͳ��ͼ�ṩ����Ϣ������������⣺

(1)�˴ε����ѧ������Ϊ___��
(2)����ͳ��ͼ�д��ڴ������___(��A. B.C�е�һ��)������ͼ�м��Ը�����
(3)��ͼ2�в�������ͳ��ͼ�в������IJ��֣�
(4)�����У��600��ѧ������ô�Դ˻���dz�ϲ���������Ƚ�ϲ������ѧ�����ж�����?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
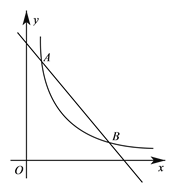
����Ŀ����ͼ��ֱ��y=��x+6�뷴��������y=![]() ��x��0����ͼ����A��3��
��x��0����ͼ����A��3��![]() ��a����B����.
��a����B����.
��1����k��ֵ;
��2��ֱ��x=m��ֱ��AB�ཻ�ڵ�M���뷴����������ͼ���ཻ�ڵ�N����MN=1����m��ֵ��
��3��ֱ��д������ʽ![]() ��
��![]() x�Ľ⼯��
x�Ľ⼯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ���ϣ�����ʦ������������
��ͼ1����ABC�У�BC��AB��AC����BC����ȡһ��P��ʹ��APC=2��ABC��
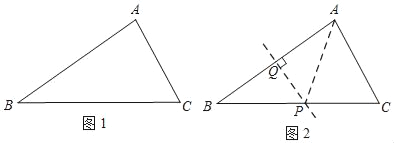
С·���������£���ͼ2��
����AB�ߵĴ�ֱƽ���ߣ���BC�ڵ�P��
������AP��
���ԣ���APC=2��ABC��
С·����ͼ������_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪![]() ��
��![]() ��
��![]() ƽ��
ƽ��![]() ��
��

(1)��![]() ����
����![]() _______����
_______����![]() _______����
_______����
(2)��![]() ����
����![]() ________����
________����![]() ________����
________����
(3)��![]() ��
��![]() ����ֱ��д��
����ֱ��д��![]() ��
��![]() ֮���������ϵ��
֮���������ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������˵������ƽ���ı��μ������ĶԳ�ͼ�Σ�������Գ�ͼ�Σ����������������Գ����ƽ���ı������������ڽǵĺ͵���![]() �������ε�������㹫ʽ�����ˡ�
�������ε�������㹫ʽ�����ˡ�![]() �ס��ߡ�֮�⣬���С�
�ס��ߡ�֮�⣬���С�![]() ���Խ���֮�������ݾ��κ����ξ��������ƽ���ı��Σ���˾���ƽ���ı��ε���������.������ȷ�Ľ��۵ĸ����У� ��
���Խ���֮�������ݾ��κ����ξ��������ƽ���ı��Σ���˾���ƽ���ı��ε���������.������ȷ�Ľ��۵ĸ����У� ��
A. 1B. 2C. 3D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪һ�κ���![]() ��ͼ�����
��ͼ�����![]() ��
��![]() ��ֱ�߽��ڵ�P����x�ᡢy��ֱ��ཻ�ڵ�C�͵�D��
��ֱ�߽��ڵ�P����x�ᡢy��ֱ��ཻ�ڵ�C�͵�D��
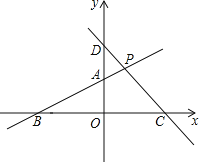
![]() ��ֱ��AB�Ľ���ʽ����P�����ꣻ
��ֱ��AB�Ľ���ʽ����P�����ꣻ
![]() ����AC����
����AC����![]() �������
�������
![]() ���E��x���ϣ�����C��D���ɵ��������Σ���ֱ��д����E�����꣮
���E��x���ϣ�����C��D���ɵ��������Σ���ֱ��д����E�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����ƺ�ķ�������100����״��ͬ���������ι�����ɣ�Ϊ���ι������ÿ�λ�����Ҫ���0.4m����һ������ֵ�֧��������������ߵ��ײ�0.5m����ͼ������������������Ҫ�����֧�����ܳ�������Ϊ��������
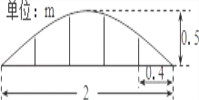
A. 50m B. 100m C. 160m D. 200m
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com