
【题目】如图,已知![]() ,
,![]() ,
,![]() 平分
平分![]() .
.

(1)若![]() ,则
,则![]() _______°,
_______°,![]() _______°;
_______°;
(2)若![]() ,则
,则![]() ________°,
________°,![]() ________°;
________°;
(3)若![]() ,
,![]() ,请直接写出
,请直接写出![]() 与
与![]() 之间的数量关系.
之间的数量关系.
【答案】(1)55,40;(2)70,20;(3)β=2α-30°.
【解析】
(1)根据余角的定义即可求出∠BOC,根据角平分线的定义求出∠MOB,即可求出∠NOB;
(2)根据角的和差求出∠MOB,再根据角平分线的定义即可求出∠BOC,然后根据余角的定义即可求出∠AOC;
(3)根据余角的定义表示出∠BOC,再根据角平分线的定义表示出∠MOB,然后根据角的和差即可得出α与β之间的数量关系.
(1)∠BOC=∠AOB-∠AOC=90°-35°=55°;
∵OC平分∠MOB,
∴∠MOB=2∠BOC=110°,
∴∠NOB=∠MON-∠MOB=150°-110°=40°.
故答案为:55,40;
(2)∠MOB=∠MON-∠NOB=150°-10°=140°,
∵OC平分∠MOB,
∴∠BOC=![]() ∠MOB=70°;
∠MOB=70°;
∴∠AOC=90°-∠BOC=20°.
故答案为70,20;
(3)∵∠AOC=α,∠NOB=β,
∴∠BOC=90°-α,
∵OC平分∠MOB,
∴∠MOB=2∠BOC=180°-2α,
∵∠MOB+∠NOB=150°,
∴180°-2α+β=150°,
即β=2α-30°.


 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】数轴上两个质点A.B所对应的数为8、4,A.B两点各自以一定的速度在数轴上运动,且A点的运动速度为2个单位/秒。
![]()
(1)点A.B两点同时出发相向而行,在4秒后相遇,求B点的运动速度;
(2)A、B两点以(1)中的速度同时出发,向数轴正方向运动,几秒钟时两者相距6个单位长度;
(3)A、B两点以(1)中的速度同时出发,向数轴负方向运动,与此同时,C点从原点出发作同方向的运动,且在运动过程中,始终有CA=2CB,若干秒钟后,C停留在10处,求此时B点的位置?
查看答案和解析>>
科目:初中数学 来源: 题型:
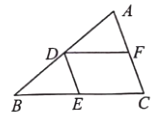
【题目】如图,在△ABC中,D、E、F分别为边AB、BC、CA的中点.
(1)求证:四边形DECF是平行四边形.
(2)当AC、BC满足何条件时,四边形DECF为菱形?
查看答案和解析>>
科目:初中数学 来源: 题型:
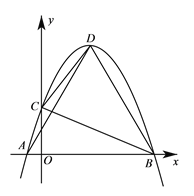
【题目】如图,抛物线y=-![]()
![]() +mx+m+
+mx+m+![]() 与x轴相交于点A、B(点A在B的左侧)与y轴相交于点C,顶点D在第一象限.
与x轴相交于点A、B(点A在B的左侧)与y轴相交于点C,顶点D在第一象限.
(1)求顶点D的坐标(用m 的代数式表示);
(2)当60°≤∠ADB≤90°时,求m的变化范围;
(3)当△BCD的面积与△ABC的面积相等时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
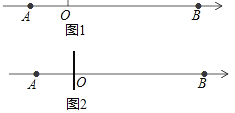
【题目】如图1,在数轴上A点表示数a,B点表示数b,AB表示A点和B点之间的距离,且a、b满足|a+4|+|b+3a|=0.
(1)求A、B两点之间的距离;
(2)若在数轴上存在一点C,且AC+BC=19,求C点表示的数;
(3)如图2,若在原点O处放一挡板,一小球甲从点A处以2个单位/秒的速度向左运动;两秒后另一个小球乙从点B处以3个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看做一点)乙球以4个单位/秒的速度向相反方向运动,设甲球运动的时间为t(秒).
①分别表示甲、乙两小球到原点的距离(用含t的式子表示);
②求甲、乙两小球到原点的距离相等时,甲球所在位置对应的数;
查看答案和解析>>
科目:初中数学 来源: 题型:
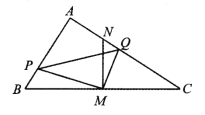
【题目】在△ABC 中,∠BAC=90°,AB<AC,M 是 BC 边的中点,MN⊥BC交 AC 于点 N,动点 P 在线段 BA 上以每秒![]() cm 的速度由点 B 向点 A 运动.同时, 动点 Q 在线段 AC 上由点 N 向点 C 运动,且始终保持 MQ⊥MP. 一个点到终点时,两个点同时停止运动.设运动时间为 t 秒(t>0).
cm 的速度由点 B 向点 A 运动.同时, 动点 Q 在线段 AC 上由点 N 向点 C 运动,且始终保持 MQ⊥MP. 一个点到终点时,两个点同时停止运动.设运动时间为 t 秒(t>0).
(1)△PBM 与△QNM 相似吗?请说明理由;
(2)若∠ABC=60°,AB=4 ![]() cm.
cm.
①求动点 Q 的运动速度;
②设△APQ 的面积为 s(cm2),求 S 与 t 的函数关系式.(不必写出 t 的取值范围)
(3)探求 BP、PQ、CQ 三者之间的数量关系,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
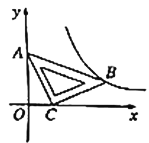
【题目】在平面直角坐标系![]() 中,将一块含有
中,将一块含有![]() 角的直角三角板如图放置,直角顶点
角的直角三角板如图放置,直角顶点![]() 的坐标为
的坐标为![]() ,顶点
,顶点![]() 的坐标为
的坐标为![]() ,顶点
,顶点![]() 恰好落在第一象限的双曲线上,现将直角三角板沿
恰好落在第一象限的双曲线上,现将直角三角板沿![]() 轴正方向平移,当顶点
轴正方向平移,当顶点![]() 恰好落在该双曲线上时停止运动,则此时点
恰好落在该双曲线上时停止运动,则此时点![]() 的对应点
的对应点![]() 的坐标为( )
的坐标为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=mx2﹣4mx+4m+4(m≠0)的顶点为P.P,M两点关于原点O成中心对称.
(1)求点P,M的坐标;
(2)若该抛物线经过原点,求抛物线的表达式;
(3)在(2)的条件下,将抛物线沿x轴翻折,翻折后的图象在0≤x≤5的部分记为图象H,点N为抛物线对称轴上的一个动点,经过M,N的直线与图象H有两个公共点,结合图象求出点N的纵坐标n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十一”黄金周期间,某市在![]() 天中外出旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
天中外出旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
日期 |
|
|
|
|
|
|
|
人数变化(万人) |
|
|
|
|
|
|
|
(1)若![]() 月
月![]() 日外出旅游人数为
日外出旅游人数为![]() ,那么
,那么![]() 月
月![]() 日外出旅游的人数是多少?
日外出旅游的人数是多少?
(2)请判断七天内外出旅游人数最多的是哪天?最少的是哪天?它们相差多少?
(3)如果最多一天有出游人数![]() 万人,那么若
万人,那么若![]() 月
月![]() 日外出旅游的有多少人?
日外出旅游的有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com