
【题目】如图,在平面直角坐标系中,已知一次函数![]() 的图象与过
的图象与过![]() 、
、![]() 的直线交于点P,与x轴、y轴分别相交于点C和点D.
的直线交于点P,与x轴、y轴分别相交于点C和点D.
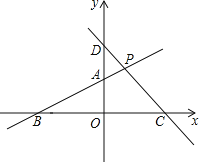
![]() 求直线AB的解析式及点P的坐标;
求直线AB的解析式及点P的坐标;
![]() 连接AC,求
连接AC,求![]() 的面积;
的面积;
![]() 设点E在x轴上,且与C、D构成等腰三角形,请直接写出点E的坐标.
设点E在x轴上,且与C、D构成等腰三角形,请直接写出点E的坐标.
【答案】(1)![]() ,,P
,,P![]() (2)
(2)![]() ;(3)点E的坐标为
;(3)点E的坐标为![]() 、
、![]() 、
、![]() 或
或![]() .
.
【解析】
(1)由点A、B的坐标,利用待定系数法即可求出直线AB的解析式,再联立直线AB、CD的解析式成方程组,通过解方程组可求出点P的坐标;
(2)过点P作PM⊥BC于点M,利用一次函数图象上点的坐标特征可求出点C的坐标,结合点A、B、P的坐标,可得出BC、OA、PM的值,利用三角形的面积公式结合S△PAC=S△PBC-S△ABC即可求出△PAC的面积;
(3)利用一次函数图象上点的坐标特征可得出点C、D的坐标,进而可得出CD的长度,分DE=DC、CD=CE、EC=ED三种情况求出点E的坐标,此题得解.
![]() 设直线AB的解析式为
设直线AB的解析式为![]() ,
,
将![]() 、
、![]() 代入
代入![]() ,得:
,得:
![]() ,解得:
,解得:
![]() 直线AB的解析式为
直线AB的解析式为![]() .
.
联立直线AB、CD的解析式成方程组,得:
 ,解得:
,解得: ,
,
![]() 点P的坐标为
点P的坐标为![]()
![]() 过点P作
过点P作![]() 于点M,如图1所示.
于点M,如图1所示.
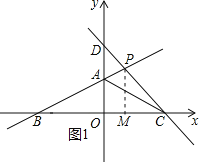
![]() 点P的坐标为
点P的坐标为![]() ,
,
![]() .
.
![]() 一次函数
一次函数![]() 的图象与x轴交于点C,
的图象与x轴交于点C,
![]() 点C的坐标为
点C的坐标为![]() ,
,
![]() .
.
![]() 点A的坐标为
点A的坐标为![]() ,点B的坐标为
,点B的坐标为![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
 .
.
![]() 为等腰三角形,
为等腰三角形,
![]() 或
或![]() 或
或![]() 如图
如图![]() .
.
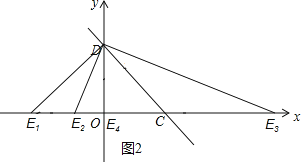
![]() 一次函数
一次函数![]() 的图象与x轴、y轴分别相交于点C和点D,
的图象与x轴、y轴分别相交于点C和点D,
![]() 点C的坐标为
点C的坐标为![]() ,点D的坐标为
,点D的坐标为![]() ,
,
![]() ,
,![]() .
.
![]() 当
当![]() 时,
时,![]() ,
,
![]() ,
,
![]() 点E的坐标为
点E的坐标为![]() ;
;
![]() 当
当![]() 时,
时,![]() ,
,
![]() 点E的坐标为
点E的坐标为![]() 或
或![]() ;
;
![]() 当
当![]() 时,点E与点O重合,
时,点E与点O重合,
![]() 点E的坐标为
点E的坐标为![]() .
.
综上所述:点E的坐标为![]() 、
、![]() 、
、![]() 或
或![]() .
.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
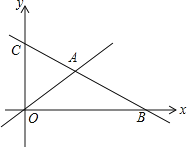
【题目】如图,在平面直角坐标系中,直线![]() :
:![]() 分别与x轴、y轴交于点B、C,且与直线
分别与x轴、y轴交于点B、C,且与直线![]() :
:![]() 交于点A.
交于点A.
![]() 分别求出点A、B、C的坐标;
分别求出点A、B、C的坐标;
![]() 直接写出关于x的不等式
直接写出关于x的不等式![]() 的解集;
的解集;
![]() 若D是线段OA上的点,且
若D是线段OA上的点,且![]() 的面积为12,求直线CD的函数表达式.
的面积为12,求直线CD的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了经济发展的需要,某市2014年投入科研经费500万元,2016年投入科研经费720万元.
(1)求2014至2016年该市投入科研经费的年平均增长率;
(2)根据目前经济发展的实际情况,该市计划2017年投入的科研经费比2016年有所增加,但年增长率不超过15%,假定该市计划2017年投入的科研经费为a万元,请求出a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
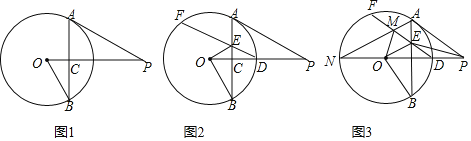
【题目】已知:PA是![]() 的切线,点B在
的切线,点B在![]() 上,连接OB,OP,连接AB交OP于点C,
上,连接OB,OP,连接AB交OP于点C,![]() .
.
![]() 如图1,求证:
如图1,求证:![]() ;
;
![]() 如图2,OP交
如图2,OP交![]() 于点D,过点D作
于点D,过点D作![]() 交AB于点E,连接OE,求证:
交AB于点E,连接OE,求证:![]() ;
;
![]() 如图3,在
如图3,在![]() 的条件下,延长PO交
的条件下,延长PO交![]() 于点N,连接AN交DF于点M,连接OM、EP,若
于点N,连接AN交DF于点M,连接OM、EP,若![]() ,
,![]() ,求线段BE的长.
,求线段BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列图形都是由面积为1的正方形按一定的规律组成,其中,图1中面积为1 的正方形有9个,图2中面积为1的正方形有14个,…,按此规律,图9中面积为1的正方形的个数为( )
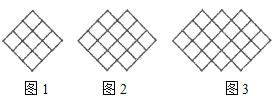 ……
……
A. 49 B. 45 C. 44 D. 40
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形纸片ABCD中,AB=3cm,AD=5cm,折叠纸片使B点落在边AD上的E处,折痕为PQ,过点E作EF∥AB交PQ于F,连接BF.
(1)求证:四边形BFEP为菱形;
(2)当点E在AD边上移动时,折痕的端点P、Q也随之移动;
①当点Q与点C重合时(如图2),求菱形BFEP的边长;
②若限定P、Q分别在边BA、BC上移动,求出点E在边AD上移动的最大距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,∠A=140°,∠D=80°.

(1)如图1,若∠B=∠C,试求出∠C的度数;
(2)如图2,若∠ABC的角平分线BE交DC于点E,且BE∥AD,试求出∠C的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学校组织的游艺晚会上,掷飞镖游戏规则如下:如图,掷到A区和B区的得分不同,A区为小圆内部分,B区为大圆内小圆外部分(掷中一次记一个点).现统计小华、小明和小芳掷中与得分情况如图所示,依此方法计算小芳的得分为( )

A. 76分 B. 74分 C. 72分 D. 70分
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com