
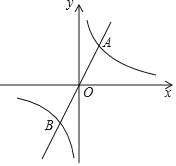
【题目】如图,已知正比例函数y=2x与反比例函数y=![]() (k>0)的图象交于A、B两点,且点A的横坐标为4,
(k>0)的图象交于A、B两点,且点A的横坐标为4,
(1)求k的值;
(2)根据图象直接写出正比例函数值小于反比例函数值时x的取值范围;
(3)过原点O的另一条直线l交双曲线y=![]() (k>0)于P、Q两点(P点在第一象限),若由点A、P、B、Q为顶点组成的四边形面积为224,求点P的坐标.
(k>0)于P、Q两点(P点在第一象限),若由点A、P、B、Q为顶点组成的四边形面积为224,求点P的坐标.
【答案】(1) k=32 (2) x<﹣8或0<x<8 (3) P(﹣7+3![]() ,16+
,16+![]() );或P(7+3
);或P(7+3![]() ,﹣16+
,﹣16+![]() )
)
【解析】分析:(1)先将x=4代入正比例函数y=2x,可得出y=8,求得点A(4,8),再根据点A与B关于原点对称,得出B点坐标,即可得出k的值;
(2)正比例函数的值小于反比例函数的值即正比例函数的图象在反比例函数的图象下方,根据图形可知在交点的右边正比例函数的值小于反比例函数的值.
(3)由于双曲线是关于原点的中心对称图形,因此以A、B、P、Q为顶点的四边形应该是平行四边形,那么△POA的面积就应该是四边形面积的四分之一即56.可根据双曲线的解析式设出P点的坐标,然后表示出△POA的面积,由于△POA的面积为56,由此可得出关于P点横坐标的方程,即可求出P点的坐标.
详解:(1)∵点A在正比例函数y=2x上,
∴把x=4代入正比例函数y=2x,
解得y=8,∴点A(4,8),
把点A(4,8)代入反比例函数y=![]() ,得k=32,
,得k=32,
(2)∵点A与B关于原点对称,
∴B点坐标为(﹣4,﹣8),
由交点坐标,根据图象直接写出正比例函数值小于反比例函数值时x的取值范围,x<﹣8或0<x<8;
(3)∵反比例函数图象是关于原点O的中心对称图形,
∴OP=OQ,OA=OB,
∴四边形APBQ是平行四边形,
∴S△POA=S平行四边形APBQ×=![]() ×224=56,
×224=56,
设点P的横坐标为m(m>0且m≠4),
得P(m, ![]() ),
),
过点P、A分别做x轴的垂线,垂足为E、F,
∵点P、A在双曲线上,
∴S△POE=S△AOF=16,
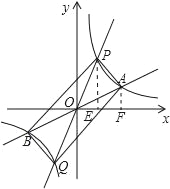
若0<m<4,如图,
∵S△POE+S梯形PEFA=S△POA+S△AOF,
∴S梯形PEFA=S△POA=56.
∴![]() (8+
(8+![]() )(4﹣m)=56.
)(4﹣m)=56.
∴m1=﹣7+3![]() ,m2=﹣7﹣3
,m2=﹣7﹣3![]() (舍去),
(舍去),
∴P(﹣7+3![]() ,16+
,16+![]() );
);
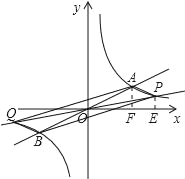
若m>4,如图,
∵S△AOF+S梯形AFEP=S△AOP+S△POE,
∴S梯形PEFA=S△POA=56.
∴![]() ×(8+
×(8+![]() )(m﹣4)=56,
)(m﹣4)=56,
解得m1=7+3![]() ,m2=7﹣3
,m2=7﹣3![]() (舍去),
(舍去),
∴P(7+3![]() ,﹣16+
,﹣16+![]() ).
).
∴点P的坐标是P(﹣7+3![]() ,16+
,16+![]() );或P(7+3
);或P(7+3![]() ,﹣16+
,﹣16+![]() ).
).


科目:初中数学 来源: 题型:
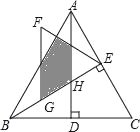
【题目】如图,△ABC是等边三角形,高AD、BE相交于点H,BC=4![]() ,在BE上截取BG=2,以GE为边作等边三角形GEF,则△ABH与△GEF重叠(阴影)部分的面积为_____.
,在BE上截取BG=2,以GE为边作等边三角形GEF,则△ABH与△GEF重叠(阴影)部分的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)23﹣17﹣(﹣7)+(﹣16)
(2)![]()
(3)﹣22÷(﹣4)3+|0.8﹣1|×(2![]() )2
)2
(4)4xy+(3y2﹣2x2)﹣(5xy﹣2x2)﹣4y2
(5)先化简,再求值:![]() x﹣2(x﹣y2)+(﹣
x﹣2(x﹣y2)+(﹣![]() x+
x+![]() y2),其中x=﹣
y2),其中x=﹣![]() ,y=3
,y=3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,∠BAC=90°,AB=AC,D 是 AC 边上一动点, CE⊥BD 于 E.
(1)如图(1),若 BD 平分∠ABC 时,①求∠ECD 的度数;②求证:BD=2EC;
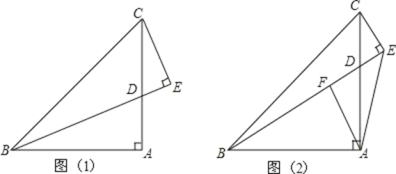
(2)如图(2),过点 A 作 AF⊥BE 于点 F,猜想线段 BE,CE,AF 之间的数量关系并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学九(1)班为了了解全班学生喜欢球类活动的情况,采取全面调查的方法,从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好,根据调查的结果组建了4个兴趣小组,并绘制成如图所示的两幅不完整的统计图(如图①,②,要求每位学生只能选择一种自己喜欢的球类),请你根据图中提供的信息解答下列问题:

(1)九(1)班的学生人数为40,并把条形统计图补充完整;
(2)扇形统计图中m=10,n=20,表示“足球”的扇形的圆心角是72度;
(3)排球兴趣小组4名学生中有3男1女,现在打算从中随机选出2名学生参加学校的排球队,请用列表或画树状图的方法求选出的2名学生恰好是1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上两个质点A.B所对应的数为8、4,A.B两点各自以一定的速度在数轴上运动,且A点的运动速度为2个单位/秒。
![]()
(1)点A.B两点同时出发相向而行,在4秒后相遇,求B点的运动速度;
(2)A、B两点以(1)中的速度同时出发,向数轴正方向运动,几秒钟时两者相距6个单位长度;
(3)A、B两点以(1)中的速度同时出发,向数轴负方向运动,与此同时,C点从原点出发作同方向的运动,且在运动过程中,始终有CA=2CB,若干秒钟后,C停留在10处,求此时B点的位置?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1:![]() ,点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.
,点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.

(1)山坡坡角(即∠ABC)的度数等于 度;
(2)求山坡A、B两点间的距离(结果精确到0.1米).
(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,AH是边BC上的高.
(1)求证:四边形ADEF是平行四边形;
(2)求证:∠DHF=∠DEF.

查看答案和解析>>
科目:初中数学 来源: 题型:
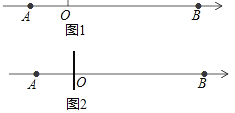
【题目】如图1,在数轴上A点表示数a,B点表示数b,AB表示A点和B点之间的距离,且a、b满足|a+4|+|b+3a|=0.
(1)求A、B两点之间的距离;
(2)若在数轴上存在一点C,且AC+BC=19,求C点表示的数;
(3)如图2,若在原点O处放一挡板,一小球甲从点A处以2个单位/秒的速度向左运动;两秒后另一个小球乙从点B处以3个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看做一点)乙球以4个单位/秒的速度向相反方向运动,设甲球运动的时间为t(秒).
①分别表示甲、乙两小球到原点的距离(用含t的式子表示);
②求甲、乙两小球到原点的距离相等时,甲球所在位置对应的数;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com