
【题目】如图,Rt△ABC中,∠ACB=90°,D是斜边AB上的中点,E是边BC上的点,AE与CD交于点F,且AC2=CECB. 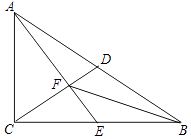
(1)求证:AE⊥CD;
(2)连接BF,如果点E是BC中点,求证:∠EBF=∠EAB.
【答案】
(1)证明:∵AC2=CECB,
∴ ![]() .
.
又∵∠ACB=∠ECA=90°
∴△ACB∽△ECA,
∴∠ABC=∠EAC.
∵点D是AB的中点,
∴CD=AD,
∴∠ACD=∠CAD
∵∠CAD+∠ABC=90°,
∴∠ACD+∠EAC=90°
∴∠AFC=90°,
∴AE⊥CD
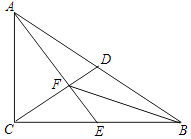
(2)证明:∵AE⊥CD,
∴∠EFC=90°,
∴∠ACE=∠EFC
又∵∠AEC=∠CEF,
∴△ECF∽△EAC
∴ ![]()
∵点E是BC的中点,
∴CE=BE,
∴ ![]()
∵∠BEF=∠AEB,
∴△BEF∽△AEB
∴∠EBF=∠EAB.
【解析】(1)先根据题意得出△ACB∽△ECA,再由直角三角形的性质得出CD=AD,由∠CAD+∠ABC=90°可得出∠ACD+∠EAC=90°,进而可得出∠AFC=90°;(2)根据AE⊥CD可得出∠EFC=90°,∠ACE=∠EFC,故可得出△ECF∽△EAC,再由点E是BC的中点可知CE=BE,故 ![]() ,根据∠BEF=∠AEB得出△BEF∽△AEB,进而可得出结论.
,根据∠BEF=∠AEB得出△BEF∽△AEB,进而可得出结论.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】一个批发商销售成本为20元/千克的某产品,根据物价部门规定:该产品每千克售价不得超过90元,在销售过程中发现的售量y(千克)与售价x(元/千克)满足一次函数关系,对应关系如下表:
售价x(元/千克) | … | 50 | 60 | 70 | 80 | … |
销售量y(千克) | … | 100 | 90 | 80 | 70 | … |
(1)求y与x的函数关系式;
(2)该批发商若想获得4000元的利润,应将售价定为多少元?
(3)该产品每千克售价为多少元时,批发商获得的利润w(元)最大?此时的最大利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣x,g(x)=ex﹣ax﹣1(e为自然对数的底数).
(1)讨论函数g(x)的单调性;
(2)当x>0时,f(x)≤g(x)恒成立,求实数a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A(1,0),B(﹣3,0)两点.
(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由;
(3)在(1)中的抛物线上的第二象限上是否存在一点P,使△PBC的面积最大?若存在,求出点P的坐标及△PBC的面积最大值;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点E在边AD上,联结CE并延长,交对角线BD于点F,交BA的延长线于点G,如果DE=2AE,那么CF:EF:EG= . 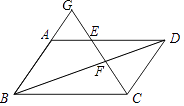
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,如果∠ADC=∠BAC,那么下列条件中不能判定△ADC和△BAC相似的是( ) 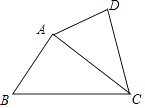
A.∠DAC=∠ABC
B.AC是∠BCD的平分线
C.AC2=BC?CD
D.![]() =
= ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com