
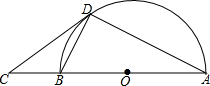
 如图,AB是半圆O的直径,C是AB延长线上的一点,CD与半圆O相切于点D,连接AD,BD.
如图,AB是半圆O的直径,C是AB延长线上的一点,CD与半圆O相切于点D,连接AD,BD.分析 (1)连接OD,利用切线的性质和直径的性质转化为角的关系进行证明即可;
(2)根据三角函数进行计算即可.
解答 证明:(1)连接OD,如图,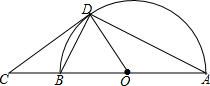
∵CD与半圆O相切于点D,
∴OD⊥CD,
∴∠CDO=90°,即∠CDB+∠BDO=90°,
∵AB是半圆O的直径,
∴∠ADB=90°,即∠ADO+∠BDO=90°,
∴∠CDB=∠ODA,
∵OD=OA,
∴∠ODA=∠BAD,
∴∠BAD=∠BDC;
(2)∵∠BAD=∠BDC=28°,在Rt△ABD中,sin∠BAD=$\frac{BD}{AB}$,
∴AB=$\frac{BD}{sin∠BAD}=\frac{2}{sin28°}≈4.260$,
∴⊙O的半径为$\frac{AB}{2}=2.13$.
点评 此题考查切线的性质,关键是根据切线的性质和直径的性质转化为角的关系进行分析.


科目:初中数学 来源: 题型:解答题
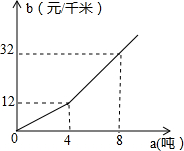 某农场急需铵肥8吨,在该农场南北方向分别有一家化肥公司A、B,A公司有铵肥3吨,每吨售价750元;B公司有铵肥7吨,每吨售价700元,汽车每千米的运输费用b(单位:元/千米)与运输重量a(单位:吨)的关系如图所示.
某农场急需铵肥8吨,在该农场南北方向分别有一家化肥公司A、B,A公司有铵肥3吨,每吨售价750元;B公司有铵肥7吨,每吨售价700元,汽车每千米的运输费用b(单位:元/千米)与运输重量a(单位:吨)的关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com