
分析 观察等式:左边的被开方数的整数部分和分数部分的分子相同,分母是分子的立方减去1;右边根号外是左边的整数部分,根号内是左边被开方数的分数部分.
解答 解:$\root{3}{(n+1)+\frac{n+1}{(n+1)^{3}-1}}$=(n+1)$\root{3}{\frac{n+1}{(n+1)^{3}-1}}$.
验证:$\root{3}{(n+1)+\frac{n+1}{(n+1)^{3}-1}}$
=$\root{3}{\frac{(n+1)[(n+1)^{3}-1+1]}{(n+1)^{3}-1}}$
=$\root{3}{\frac{(n+1)^{3}(n+1)}{(n+1)^{3}-1}}$
=(n+1)$\root{3}{\frac{n+1}{(n+1)^{3}-1}}$.
点评 此题考查了立方根,等式的规律问题,要分别观察等式的左边和右边.


科目:初中数学 来源: 题型:解答题
 如图,资江风光带有一块长100米,宽50米的草坪,要在中间铺设两横两纵且宽度一样的小路,若草坪面积恰好3600平方米,求小路的宽为多少米?
如图,资江风光带有一块长100米,宽50米的草坪,要在中间铺设两横两纵且宽度一样的小路,若草坪面积恰好3600平方米,求小路的宽为多少米?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
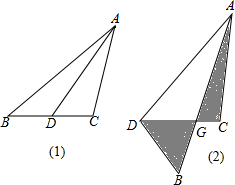
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为了了解业余射击队队员的射击成绩,对某次射击比赛中每一名队员的平均成绩(单位:环,环数为整数)进行了统计.分别绘制了统计表和成绩分布直方图,请你根据统计表和成绩分布直方图回答下列问题:
为了了解业余射击队队员的射击成绩,对某次射击比赛中每一名队员的平均成绩(单位:环,环数为整数)进行了统计.分别绘制了统计表和成绩分布直方图,请你根据统计表和成绩分布直方图回答下列问题:| 平均成绩 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 人数 | 1 | a | 3 | 3 | b | 4 | c | 6 | 1 | 0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com