
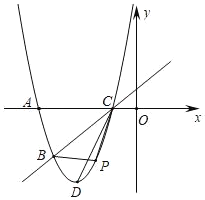
【题目】如图,已知抛物线y=ax2+bx+5经过A(﹣5,0),B(﹣4,﹣3)两点,与x轴的另一个交点为C,顶点为D,连结CD.
(1)求该抛物线的表达式;
(2)点P为该抛物线上一动点(与点B、C不重合),设点P的横坐标为t.
①当点P在直线BC的下方运动时,求△PBC的面积的最大值;
②该抛物线上是否存在点P,使得∠PBC=∠BCD?若存在,求出所有点P的坐标;若不存在,请说明理由.
【答案】(1)y=x2+6x+5;(2)①S△PBC的最大值为![]() ;②存在,点P的坐标为P(﹣
;②存在,点P的坐标为P(﹣![]() ,﹣
,﹣![]() )或(0,5).
)或(0,5).
【解析】
(1)将点A、B坐标代入二次函数表达式,即可求出二次函数解析式;
(2)①如图1,过点P作y轴的平行线交BC于点G,将点B、C的坐标代入一次函数表达式并解得:直线BC的表达式为:y=x+1,设点G(t,t+1),则点P(t,t2+6t+5),利用三角形面积公式求出最大值即可;
②设直线BP与CD交于点H,当点P在直线BC下方时,求出线段BC的中点坐标为(﹣![]() ,﹣
,﹣![]() ),过该点与BC垂直的直线的k值为﹣1,求出 直线BC中垂线的表达式为:y=﹣x﹣4…③,同理直线CD的表达式为:y=2x+2…④,、联立③④并解得:x=﹣2,即点H(﹣2,﹣2),同理可得直线BH的表达式为:y=
),过该点与BC垂直的直线的k值为﹣1,求出 直线BC中垂线的表达式为:y=﹣x﹣4…③,同理直线CD的表达式为:y=2x+2…④,、联立③④并解得:x=﹣2,即点H(﹣2,﹣2),同理可得直线BH的表达式为:y=![]() x﹣1…⑤,联立⑤和y=x2+6x+5并解得:x=﹣
x﹣1…⑤,联立⑤和y=x2+6x+5并解得:x=﹣![]() ,即可求出P点;当点P(P′)在直线BC上方时,根据∠PBC=∠BCD求出BP′∥CD,求出直线BP′的表达式为:y=2x+5,联立y=x2+6x+5和y=2x+5,求出x,即可求出P.
,即可求出P点;当点P(P′)在直线BC上方时,根据∠PBC=∠BCD求出BP′∥CD,求出直线BP′的表达式为:y=2x+5,联立y=x2+6x+5和y=2x+5,求出x,即可求出P.
解:(1)将点A、B坐标代入二次函数表达式得:![]() ,
,
解得:![]() ,
,
故抛物线的表达式为:y=x2+6x+5…①,
令y=0,则x=﹣1或﹣5,
即点C(﹣1,0);
(2)①如图1,过点P作y轴的平行线交BC于点G,
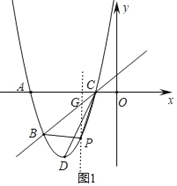
将点B、C的坐标代入一次函数表达式并解得:
直线BC的表达式为:y=x+1…②,
设点G(t,t+1),则点P(t,t2+6t+5),
S△PBC=![]() PG(xC﹣xB)=
PG(xC﹣xB)=![]() (t+1﹣t2﹣6t﹣5)=﹣
(t+1﹣t2﹣6t﹣5)=﹣![]() t2﹣
t2﹣![]() t﹣6,
t﹣6,
∵-![]() <0,
<0,
∴S△PBC有最大值,当t=﹣![]() 时,其最大值为
时,其最大值为![]() ;
;
②设直线BP与CD交于点H,
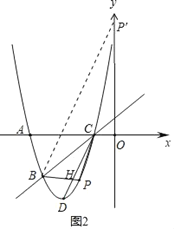
当点P在直线BC下方时,
∵∠PBC=∠BCD,
∴点H在BC的中垂线上,
线段BC的中点坐标为(﹣![]() ,﹣
,﹣![]() ),
),
过该点与BC垂直的直线的k值为﹣1,
设BC中垂线的表达式为:y=﹣x+m,将点(﹣![]() ,﹣
,﹣![]() )代入上式并解得:
)代入上式并解得:
直线BC中垂线的表达式为:y=﹣x﹣4…③,
同理直线CD的表达式为:y=2x+2…④,
联立③④并解得:x=﹣2,即点H(﹣2,﹣2),
同理可得直线BH的表达式为:y=![]() x﹣1…⑤,
x﹣1…⑤,
联立①⑤并解得:x=﹣![]() 或﹣4(舍去﹣4),
或﹣4(舍去﹣4),
故点P(﹣![]() ,﹣
,﹣![]() );
);
当点P(P′)在直线BC上方时,
∵∠PBC=∠BCD,∴BP′∥CD,
则直线BP′的表达式为:y=2x+s,将点B坐标代入上式并解得:s=5,
即直线BP′的表达式为:y=2x+5…⑥,
联立①⑥并解得:x=0或﹣4(舍去﹣4),
故点P(0,5);
故点P的坐标为P(﹣![]() ,﹣
,﹣![]() )或(0,5).
)或(0,5).


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:
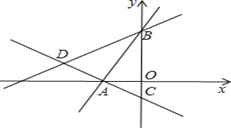
【题目】如图所示,在平面直角坐标系中,过点A(﹣![]() ,0)的两条直线分别交y轴于B、C两点,且B、C两点的纵坐标分别是一元二次方程x2﹣2x﹣3=0的两个根.
,0)的两条直线分别交y轴于B、C两点,且B、C两点的纵坐标分别是一元二次方程x2﹣2x﹣3=0的两个根.
(1)求线段BC的长度;
(2)试问:直线AC与直线AB是否垂直?请说明理由;
(3)若点D在直线AC上,且DB=DC,求点D的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 经过点
经过点![]() 、
、![]() ,且与
,且与![]() 轴交于点
轴交于点![]() ,抛物线的顶点为
,抛物线的顶点为![]() ,连接
,连接![]() ,点
,点![]() 是线段
是线段![]() 上的一个动点(不与
上的一个动点(不与![]() 、
、![]() )重合.
)重合.
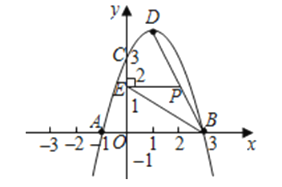
(1)求抛物线的解析式,并写出顶点![]() 的坐标;
的坐标;
(2)过点![]() 作
作![]() 轴于点
轴于点![]() ,求
,求![]() 面积的最大值及取得最大值时
面积的最大值及取得最大值时![]() 点的坐标;
点的坐标;
(3)在(2)的条件下,若点![]() 是
是![]() 轴上一动点,点
轴上一动点,点![]() 是抛物线上一动点,试判断是否存在这样的点
是抛物线上一动点,试判断是否存在这样的点![]() ,使得以点
,使得以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边若存在,请直接写出点
为顶点的四边形是平行四边若存在,请直接写出点![]() 的坐标:若不存在,请说明理由.
的坐标:若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某车库出口安装的栏杆如图所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=1.18米,AE=1.2米,那么适合该地下车库的车辆限高标志牌为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
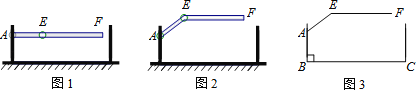
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,BD为一条对角线,AD∥BC,AD=2BC,∠ABD=90°,E为AD的中点,连接BE.
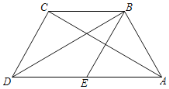
(1)求证:四边形BCDE为菱形;
(2)连接AC,若AC平分∠BAD,AB=2,求菱形BCDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我校举办的“读好书、讲礼仪”活动中,各班积极行动,图书角的新书、好书不断增多,除学校购买的图书外,还有师生捐献的图书,下面是九(1)班全体同学捐献图书情况的统计图(每人都有捐书).
请你根据以上统计图中的信息,解答下列问题:
(1)该班有学生多少人?
(2)补全条形统计图.
(3)九(1)班全体同学所捐图书是 6 本的人数在扇形统计图中所对应扇形的圆心角为多少度?
(4)请你估计全校 2000 名学生所捐图书的数量.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件10元,现在的售价为每件15元,每周可卖出100件,市场调查反映:如果每件的售价每涨1元(售价每件不能高于20元),那么每周少卖10件.设每件涨价![]() 元(
元(![]() 为非负整数),每周的销量为
为非负整数),每周的销量为![]() 件.
件.
(1)求![]() 与
与![]() 的函数关系式及自变量
的函数关系式及自变量![]() 的取值范围;
的取值范围;
(2)如果经营该商品每周的利润是560元,求每件商品的售价是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
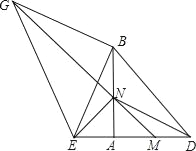
【题目】如图,等腰Rt△ABD中,AB=AD,点M 为边AD上一动点,点E在DA的延长线上,且AM=AE,以BE为直角边,向外作等腰Rt△BEG,MG交AB于N,连NE、DN.
(1)求证:∠BEN=∠BGN.
(2)求![]() 的值.
的值.
(3)当M在AD上运动时,探究四边形BDNG的形状,并证明之.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com