
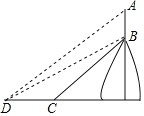
ЁОЬтФПЁПЮЛгкжиЧьЪаЛуББЧјЕФееФИЩНЩСжЙЋдАГЫГаЁАНќздШЛЁБЩњЬЌРэФюгЊдьЩСжЗчОАЃЌЁАЫфгЩШЫзїЃЌЭ№здЬьПЊЁБЃЌЭЙЯдздШЛЗчЙЧгыдЩњвАШЄЃЎЩНжазюЮЊжѕФПЕФОЕфЕБЪєРПаЧЫўЃЎЕЧСйЫўЖЅЃЌПЩЩЯОХЬьбћдТРПаЧЃЌПЩФёюЋаТЧјЃЌСьТдИННќТЅгюЕФзГУРЃЛврПЩдЖЬїСННЪЄОАЃЎЕЧСйДЫЫўЃЌШУФугаЦЎШЛШєЯЩЕФСЊЯыгжгаЕЧИпдЖЬїЃЌЁАвЛРРжкЩНаЁЁБЕФе№КГЃЌЮваЃФГЪ§бЇаЫШЄаЁзщЕФЭЌбЇзМБИРћгУЫљбЇЕФШ§НЧКЏЪ§жЊЪЖЙРВтИУЫўЕФИпЖШЃЌвбжЊРПаЧЫўABЮЛгкЦТЖШlЃН![]() :1ЕФаБЦТBCЩЯЃЌВтСПдБДгаБЦТЕзЖЫCДІЭљЧАбиЫЎЦНЗНЯђзпСЫ120mДяЕНЕиУцDДІЃЌДЫЪБВтЕУРПаЧЫўABЖЅЖЫAЕФбіНЧЮЊ37ЁуЃЌРПаЧЫўЕзЖЫBЕФбіНЧЮЊ30ЁуЃЌвбжЊAЁЂBЁЂCЁЂDдкЭЌвЛЦНУцФкЃЌдђИУЫўABЕФИпЖШЮЊЃЈЁЁЁЁЃЉmЃЌЃЈНсЙћБЃСєећЪ§ЃЌВЮПМЪ§ОнЃЛsin37ЁуЁж0.60ЃЌcos37ЁуЁж0.80ЃЌtan37ЁуЁж0.75ЃЌ
:1ЕФаБЦТBCЩЯЃЌВтСПдБДгаБЦТЕзЖЫCДІЭљЧАбиЫЎЦНЗНЯђзпСЫ120mДяЕНЕиУцDДІЃЌДЫЪБВтЕУРПаЧЫўABЖЅЖЫAЕФбіНЧЮЊ37ЁуЃЌРПаЧЫўЕзЖЫBЕФбіНЧЮЊ30ЁуЃЌвбжЊAЁЂBЁЂCЁЂDдкЭЌвЛЦНУцФкЃЌдђИУЫўABЕФИпЖШЮЊЃЈЁЁЁЁЃЉmЃЌЃЈНсЙћБЃСєећЪ§ЃЌВЮПМЪ§ОнЃЛsin37ЁуЁж0.60ЃЌcos37ЁуЁж0.80ЃЌtan37ЁуЁж0.75ЃЌ![]() Ёж1.73ЃЉ
Ёж1.73ЃЉ
A.31B.40C.60D.136
ЁОД№АИЁПA
ЁОНтЮіЁП
ЩшABЁЭDCгкEЃЌЩшCEЃНxmЃЌдђBEЃН![]() xmЃЌИљОнDC=120mПЩЯШСаГіЗНГЬЧѓГіxЕФжЕЃЌДгЖјЕУГіBEЃЌDEЕФГЄЃЌдкRtЁїADEжаПЩЧѓГіAEЕФГЄЃЌДгЖјгЩAB=AE-BEПЩЕУЕННсТлЃЎ
xmЃЌИљОнDC=120mПЩЯШСаГіЗНГЬЧѓГіxЕФжЕЃЌДгЖјЕУГіBEЃЌDEЕФГЄЃЌдкRtЁїADEжаПЩЧѓГіAEЕФГЄЃЌДгЖјгЩAB=AE-BEПЩЕУЕННсТлЃЎ
НтЃКШчЭМЃЌЩшABЁЭDCгкEЃЌ
ЩшCEЃНxmЃЌдђBEЃН![]() xmЃЌ
xmЃЌ
дкRtЁїBDEжаЃЌЁпЁЯBDEЃН30ЁуЃЌ
ЁрDEЃН![]() ЃН
ЃН![]() ЃН3xЃЌ
ЃН3xЃЌ
ЁрDCЃНDEЉCEЃН3xЉxЃН120ЃЌ
ЁрxЃН60ЃЌ
ЁрBEЃН60![]() mЃЌDEЃН180mЃЌ
mЃЌDEЃН180mЃЌ
дкRtЁїADEжаЃЌAEЃНDEtan37ЁуЁж180ЁС0.75ЃН135ЃЈmЃЉЃЌ
ЁрABЃНAEЉBEЃН135Љ60![]() Ёж31(m)ЃЌ
Ёж31(m)ЃЌ
ЙЪбЁЃКAЃЎ


 ЬиИпМЖНЬЪІЕуВІЯЕСаД№АИ
ЬиИпМЖНЬЪІЕуВІЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
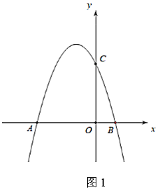
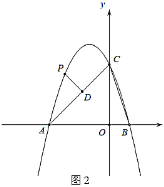
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпyЃНax2+bx+cЃЈaЁй0ЃЉгыyжсНЛгкЕуCЃЌгыxжсНЛгкAЃЌBСНЕуЃЌЦфжаЕуBЕФзјБъЮЊBЃЈ4ЃЌ0ЃЉЃЌХзЮяЯпЕФЖдГЦжсНЛxжсгкЕуDЃЌCEЁЮABЃЌВЂгыХзЮяЯпЕФЖдГЦжсНЛгкЕуEЃЎЯжгаЯТСаНсТлЃКЂйaЃО0ЃЛЂкbЃО0ЃЛЂл4a+2b+cЃМ0ЃЛЂмAD+CEЃН4ЃЎЦфжаЫљгае§ШЗНсТлЕФађКХЪЧЁЁ_____________________ ЁЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
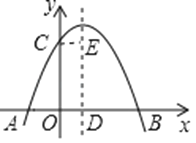
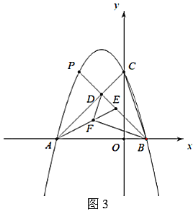
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌЕу
жаЃЌЕу![]() ЮЊзјБъдЕуЃЎХзЮяЯп
ЮЊзјБъдЕуЃЎХзЮяЯп![]() ЗжБ№НЛ
ЗжБ№НЛ![]() жсгк
жсгк![]() ЁЂ
ЁЂ![]() СНЕуЃЌНЛ
СНЕуЃЌНЛ![]() жсгкЕу
жсгкЕу![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓИУХзЮяЯпЕФНтЮіЪНЃЎ
ЃЈ2ЃЉШчЭМ2ЃЌЕу![]() ЮЊЕкЖўЯѓЯоХзЮяЯпЩЯвЛЕуЃЌЙ§Еу
ЮЊЕкЖўЯѓЯоХзЮяЯпЩЯвЛЕуЃЌЙ§Еу![]() зї
зї![]() гкЕу
гкЕу![]() ЃЌЩшЕу
ЃЌЩшЕу![]() ЕФКсзјБъЮЊ
ЕФКсзјБъЮЊ![]() ЃЌЯпЖЮ
ЃЌЯпЖЮ![]() ЕФГЄЖШЮЊ
ЕФГЄЖШЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕЪНЃЈВЛвЊЧѓаДГіздБфСП
ЕФКЏЪ§ЙиЯЕЪНЃЈВЛвЊЧѓаДГіздБфСП![]() ЕФШЁжЕЗЖЮЇЃЉЃЛ
ЕФШЁжЕЗЖЮЇЃЉЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЕБжБЯп![]() ОЙ§Еу
ОЙ§Еу![]() ЪБЃЌШчЭМ3ЃЌЕу
ЪБЃЌШчЭМ3ЃЌЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯЃЌЕу
ЩЯЃЌЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯЃЌЧв
ЩЯЃЌЧв![]() ЃЌ
ЃЌ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФГЄЃЎ
ЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊABЪЧ![]() ЕФжБОЖЃЌЕуPдкBAЕФбгГЄЯпЩЯЃЌPDЧа
ЕФжБОЖЃЌЕуPдкBAЕФбгГЄЯпЩЯЃЌPDЧа![]() гкЕуDЃЌЙ§ЕуBзї
гкЕуDЃЌЙ§ЕуBзї![]() ЃЌНЛPDЕФбгГЄЯпгкЕуCЃЌСЌНгADВЂбгГЄЃЌНЛBEгкЕуEЃЎ
ЃЌНЛPDЕФбгГЄЯпгкЕуCЃЌСЌНгADВЂбгГЄЃЌНЛBEгкЕуEЃЎ
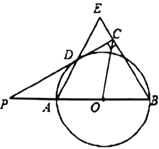
(Ђё)ЧѓжЄЃКAB=BEЃЛ
(Ђђ)СЌНсOCЃЌШчЙћPD=2![]() ЃЌЁЯABC=60ЁуЃЌЧѓOCЕФГЄЃЎ
ЃЌЁЯABC=60ЁуЃЌЧѓOCЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
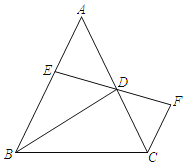
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌдкЁїABCжаABЃНACЃЌBDЦНЗжЁЯABCНЛACгкЕуDЃЌDEЦНЗжЁЯADBНЛABгкЕуEЃЌCFЁЮABНЛEDЕФбгГЄЯпгкFЃЌШєЁЯAЃН52ЁуЃЌЧѓЁЯDFCЕФЖШЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊ![]() ЃЌЕу
ЃЌЕу![]() дкБп
дкБп![]() ЩЯЃЌ
ЩЯЃЌ![]() .Й§Еу
.Й§Еу![]() зї
зї![]() гкЕу
гкЕу![]() ЃЌвд
ЃЌвд![]() ЮЊвЛБпдк
ЮЊвЛБпдк![]() ФкзїЕШБп
ФкзїЕШБп![]() ЃЌЕу
ЃЌЕу![]() ЪЧ
ЪЧ![]() ЮЇГЩЕФЧјгђЃЈАќРЈИїБпЃЉФкЕФвЛЕуЃЌЙ§Еу
ЮЇГЩЕФЧјгђЃЈАќРЈИїБпЃЉФкЕФвЛЕуЃЌЙ§Еу![]() зї
зї![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌзї
ЃЌзї![]() НЛ
НЛ![]() гкЕу
гкЕу![]() .Щш
.Щш![]() ЃЌ
ЃЌ![]() ЃЌдђ
ЃЌдђ![]() зюДѓжЕЪЧ_______.
зюДѓжЕЪЧ_______.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
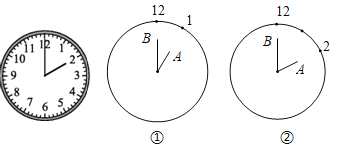
ЁОЬтФПЁПШчЭМЃЌгавЛЪБжгЃЌЪБеыOAГЄЮЊ6cmЃЌЗжеыOBГЄЮЊ8cmЃЌЁїOABЫцзХЪБМфЕФБфЛЏВЛЭЃЕиИФБфаЮзДЃЎЧѓЃК
ЃЈ1ЃЉШчЭМЂйЃЌ13ЕуЪБЃЌЁїOABЕФУцЛ§ЪЧЖрЩйЃП
ЃЈ2ЃЉШчЭМЂкЃЌ14ЕуЪБЃЌЁїOABЕФУцЛ§БШ13ЕуЪБдіДѓСЫЛЙЪЧМѕЩйСЫЃПЮЊЪВУДЃП
ЃЈ3ЃЉЮЪЖрЩйећЕуЪБЃЌЁїOABЕФУцЛ§зюДѓЃПзюДѓУцЛ§ЪЧЖрЩйЃПЧыЫЕУїРэгЩЃЎ
ЃЈ4ЃЉЩшЁЯBOAЃНІСЃЈ0ЁуЁмІСЁм180ЁуЃЉЃЌЪдЙщФЩІСБфЛЏЪБЁїOABЕФУцЛ§гаКЮБфЛЏЙцТЩЃЈВЛжЄУїЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
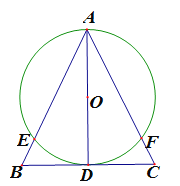
ЁОЬтФПЁПШчЭМЃЌЁїABCжаЃЌAB=ACЃЌADЁЭBCгкDЃЌвдADЮЊжБОЖЕФЁбOНЛABгкEЃЌНЛACгкFЃЎ
ЃЈ1ЃЉЧѓжЄЃКBE=CFЃЛ
ЃЈ2ЃЉШєAE=4ЃЌBC=![]() ЃЌЧѓЁбOЕФАыОЖЃЎ
ЃЌЧѓЁбOЕФАыОЖЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com