
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() 为坐标原点.抛物线
为坐标原点.抛物线![]() 分别交
分别交![]() 轴于
轴于![]() 、
、![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,
,![]() .
.
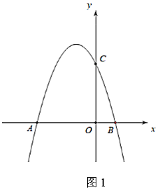
(1)求该抛物线的解析式.
(2)如图2,点![]() 为第二象限抛物线上一点,过点
为第二象限抛物线上一点,过点![]() 作
作![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,线段
,线段![]() 的长度为
的长度为![]() ,求
,求![]() 与
与![]() 的函数关系式(不要求写出自变量
的函数关系式(不要求写出自变量![]() 的取值范围);
的取值范围);
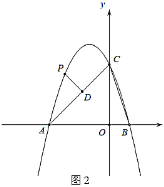
(3)在(2)的条件下,当直线![]() 经过点
经过点![]() 时,如图3,点
时,如图3,点![]() 在线段
在线段![]() 上,点
上,点![]() 在线段
在线段![]() 上,且
上,且![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 的长.
的长.
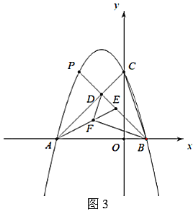
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)利用OA=OC,待定系数法求解二次函数解析式.
(2)过P作![]() 轴的垂线,用锐角三角函数建立PD与PM之间的联系,用二次函数与一次函数求解PM的长度,从而得到答案.
轴的垂线,用锐角三角函数建立PD与PM之间的联系,用二次函数与一次函数求解PM的长度,从而得到答案.
(3)延长DF交AB于N,过F,D作好AB的垂线,利用面积与相似三角形求解FN,,DN的数量关系,再利用![]() ,找到
,找到![]() ,利用相似三角形性质表示AN的长,最后化归到直角三角形DNQ中,利用勾股定理得到答案.
,利用相似三角形性质表示AN的长,最后化归到直角三角形DNQ中,利用勾股定理得到答案.
解:(1)因为:![]() ,
,
所以点C![]() ,所以
,所以![]() ,
,
又因为![]()
所以![]() ,把
,把![]() 代入解析式得:
代入解析式得:
![]() ,即
,即![]()
解得:![]() (舍去),所以
(舍去),所以![]() ,
,
所以抛物线为![]()
(2)如图,过P作![]() 轴与N,交AC于M,又
轴与N,交AC于M,又![]() ,
,![]()
所以![]() .
.
因为![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]()
所以![]()
由(1)得![]() ,所以 直线AC为
,所以 直线AC为![]() ,
,
因为![]() ,
,![]() 轴,
轴,
所以![]()
所以![]()
所以![]()
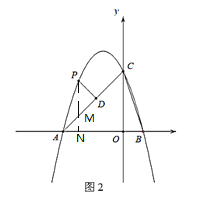
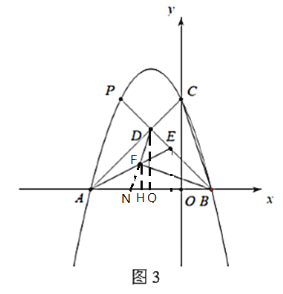
(3)如图,延长DF交AB于N,过F,D分别作![]() ,垂足分别为H,Q,因为抛物线为
,垂足分别为H,Q,因为抛物线为![]() ,所以B(1,0),A(-3,0)
,所以B(1,0),A(-3,0)
所以AB=4,因为![]() 的面积为
的面积为![]() ,
,
所以![]() ,所以
,所以![]() ,
,
因为A(-3,0),C(0,-3),![]()
所以![]()
因为![]()
所以![]()
所以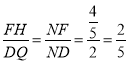
设![]() ,则
,则![]()
因为![]() ,
,![]() ,
,
所以![]()
所以![]() ,
,
又因为![]()
所以![]()
所以![]() 所以
所以![]() ,
,
所以![]()
在直角三角形DNQ中,![]()
所以![]()
解得:![]() ,(负根舍去)
,(负根舍去)
所以![]()


科目:初中数学 来源: 题型:
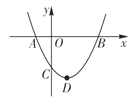
【题目】如图,二次函数![]() (
(![]() )图象的顶点为
)图象的顶点为![]() ,其图象与
,其图象与![]() 轴的交点
轴的交点![]() ,
,![]() 的横坐标分别为
的横坐标分别为![]() 和3.下列结论:
和3.下列结论:
①![]() ;②
;②![]() ;③
;③![]() ;④当
;④当![]() 时,
时,![]() 是等腰直角三角形.其中结论正确的个数是( )
是等腰直角三角形.其中结论正确的个数是( )
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线![]() 与
与![]() 轴交于点
轴交于点![]() ,且过抛物线
,且过抛物线![]() 的顶点
的顶点![]() 和抛物线上的另一点
和抛物线上的另一点![]() .
.
(1)若点![]()
①求抛物线解析式;
②若![]() ,求直线解析式.
,求直线解析式.
(2)若![]() ,过点
,过点![]() 作
作![]() 轴的平行线与抛物线的对称轴交于点
轴的平行线与抛物线的对称轴交于点![]() ,当
,当![]() 时,求
时,求![]() 的面积
的面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
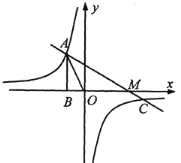
【题目】如图,已知反比例函数 y=![]() 的图像经过点A(-1,a),过点A作AB⊥x轴,垂足为点B,△AOB的面积为
的图像经过点A(-1,a),过点A作AB⊥x轴,垂足为点B,△AOB的面积为![]() .
.
(1)求a、k的值;
(2)若一次函数y=mx+n图像经过点A和反比例函数图像上另一点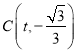 ,且与x轴交于M点,求AM的值:
,且与x轴交于M点,求AM的值:
(3)在(2)的条件下,如果以线段AM为一边作等边△AMN,顶点N在一次数函数y=bx上,则b= ______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级有1200名学生,在体育考试前随机抽取部分学生进行跳绳测试,根据测试成绩制作了下面两个统计图.请根据相关信息,解答下列问题:

(Ⅰ)本次参加跳绳测试的学生人数为___________,图①中![]() 的值为___________;
的值为___________;
(Ⅱ)求本次调查获取的样本数据的平均数、众数和中位数;
(Ⅲ)根据样本数据,估计该校九年级跳绳测试中得3分的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店计划进A,B两种水果共140千克,这两种水果的进价和售价如表所示
进价 | 售价 | |
A种水果 | 5 | 8 |
B种水果 | 9 | 13 |
![]() 若该水果店购进这两种水果共花费1020元,求该水果店分别购进A,B两种水果各多少千克?
若该水果店购进这两种水果共花费1020元,求该水果店分别购进A,B两种水果各多少千克?
![]() 在
在![]() 的基础上,为了迎接春节的来临,水果店老板决定把A种水果全部八折出售,B种水果全部降价
的基础上,为了迎接春节的来临,水果店老板决定把A种水果全部八折出售,B种水果全部降价![]() 出售,那么售完后共获利多少元?
出售,那么售完后共获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
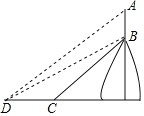
【题目】位于重庆市汇北区的照母山森林公园乘承“近自然”生态理念营造森林风景,“虽由人作,宛自天开”,凸显自然风骨与原生野趣.山中最为瞩目的经典当属揽星塔.登临塔顶,可上九天邀月揽星,可鸟瞰新区,领略附近楼宇的壮美;亦可远眺两江胜景.登临此塔,让你有飘然若仙的联想又有登高远眺,“一览众山小”的震撼,我校某数学兴趣小组的同学准备利用所学的三角函数知识估测该塔的高度,已知揽星塔AB位于坡度l=![]() :1的斜坡BC上,测量员从斜坡底端C处往前沿水平方向走了120m达到地面D处,此时测得揽星塔AB顶端A的仰角为37°,揽星塔底端B的仰角为30°,已知A、B、C、D在同一平面内,则该塔AB的高度为( )m,(结果保留整数,参考数据;sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,
:1的斜坡BC上,测量员从斜坡底端C处往前沿水平方向走了120m达到地面D处,此时测得揽星塔AB顶端A的仰角为37°,揽星塔底端B的仰角为30°,已知A、B、C、D在同一平面内,则该塔AB的高度为( )m,(结果保留整数,参考数据;sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() ≈1.73)
≈1.73)
A.31B.40C.60D.136
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形![]() 中,
中,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
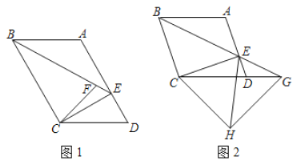
(1)如图1,点![]() 是
是![]() 上一点,连接
上一点,连接![]() ,若
,若![]() ,
,![]() ,
,![]() ,求
,求![]() 的长;
的长;
(2)如图2,若![]() ,延长
,延长![]() 交
交![]() 延长线于点
延长线于点![]() ,以
,以![]() 为斜边做等腰直角
为斜边做等腰直角![]() ,连接
,连接![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com