
【题目】如图,在平行四边形![]() 中,
中,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
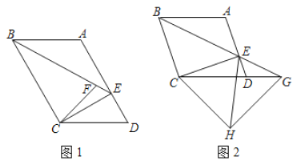
(1)如图1,点![]() 是
是![]() 上一点,连接
上一点,连接![]() ,若
,若![]() ,
,![]() ,
,![]() ,求
,求![]() 的长;
的长;
(2)如图2,若![]() ,延长
,延长![]() 交
交![]() 延长线于点
延长线于点![]() ,以
,以![]() 为斜边做等腰直角
为斜边做等腰直角![]() ,连接
,连接![]() ,求证:
,求证:![]() .
.
【答案】(1)EF=![]() ﹣4;(2)见详解
﹣4;(2)见详解
【解析】
(1)先利用勾股定理得出CE=![]() ,然后在Rt△BCE中,依据勾股定理可得
,然后在Rt△BCE中,依据勾股定理可得![]() ,进而得出EF=
,进而得出EF=![]() ﹣4;
﹣4;
(2)过C作CM⊥CG,交GH的延长线于M,连接EM,判定△BCG≌△ECM(SAS),即可得出∠CEM=∠CBG=45°,再根据H是MG的中点,即可得到Rt△MEG中,EH=![]() MG=HG.
MG=HG.
解:(1)∵平行四边形ABCD中,CE⊥BC,
∴CE⊥AD,
又∵∠ECD=30°,
∴Rt△CDE中,DE=![]() CD=1,
CD=1,
∴![]()
又∵在Rt△BCE中,BC=4,
∴![]() ,
,
∴EF=BE﹣BF=![]() ﹣4;
﹣4;
(2)如图2所示,过C作CM⊥CG,交GH的延长线于M,连接EM,
∵△CGH是等腰直角三角形,∠MCG=90°,
∴∠CGH=∠CMG=45°,
∴CG=CM,
∵∠BCE=90°,∠MCG=90°,
∴∠BCG=∠ECM,
又∵BC=EC,
∴△BCG≌△ECM(SAS),
∴∠CEM=∠CBG=45°,
又∵∠BEC=45°,
∴∠MEG=90°,
又∵CM=CG,CH平分∠MCG,
∴H是MG的中点,
∴Rt△MEG中,EH=![]() MG=HG.
MG=HG.



 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() 为坐标原点.抛物线
为坐标原点.抛物线![]() 分别交
分别交![]() 轴于
轴于![]() 、
、![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,
,![]() .
.
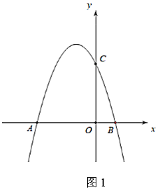
(1)求该抛物线的解析式.
(2)如图2,点![]() 为第二象限抛物线上一点,过点
为第二象限抛物线上一点,过点![]() 作
作![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,线段
,线段![]() 的长度为
的长度为![]() ,求
,求![]() 与
与![]() 的函数关系式(不要求写出自变量
的函数关系式(不要求写出自变量![]() 的取值范围);
的取值范围);
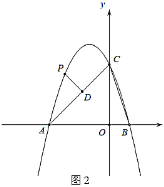
(3)在(2)的条件下,当直线![]() 经过点
经过点![]() 时,如图3,点
时,如图3,点![]() 在线段
在线段![]() 上,点
上,点![]() 在线段
在线段![]() 上,且
上,且![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,点
,点![]() 在边
在边![]() 上,
上,![]() .过点
.过点![]() 作
作![]() 于点
于点![]() ,以
,以![]() 为一边在
为一边在![]() 内作等边
内作等边![]() ,点
,点![]() 是
是![]() 围成的区域(包括各边)内的一点,过点
围成的区域(包括各边)内的一点,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,作
,作![]() 交
交![]() 于点
于点![]() .设
.设![]() ,
,![]() ,则
,则![]() 最大值是_______.
最大值是_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
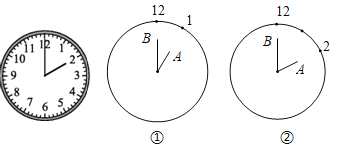
【题目】如图,有一时钟,时针OA长为6cm,分针OB长为8cm,△OAB随着时间的变化不停地改变形状.求:
(1)如图①,13点时,△OAB的面积是多少?
(2)如图②,14点时,△OAB的面积比13点时增大了还是减少了?为什么?
(3)问多少整点时,△OAB的面积最大?最大面积是多少?请说明理由.
(4)设∠BOA=α(0°≤α≤180°),试归纳α变化时△OAB的面积有何变化规律(不证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是BC的中点,点E、F分别在线段AD及其延长线上,且DE=DF,给出下列条件:①BE⊥EC;②AB=AC;③BF∥EC;从中选择一个条件使四边形BECF是菱形,你认为这个条件是_______(只填写序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
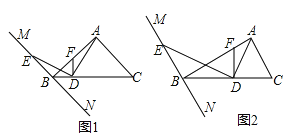
【题目】在Rt△ABC中,∠BAC=90°,过点B的直线MN∥AC,D为BC边上一点,连接AD,作DE⊥AD交MN于点E,连接AE.
(1)如图①,当∠ABC=45°时,求证:AD=DE;理由;
(2)如图②,当∠ABC=30°时,线段AD与DE有何数量关系?并请说明理由;
(3)当∠ABC=α时,请直接写出线段AD与DE的数量关系.(用含α的三角函数表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
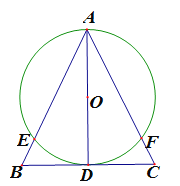
【题目】如图,△ABC中,AB=AC,AD⊥BC于D,以AD为直径的⊙O交AB于E,交AC于F.
(1)求证:BE=CF;
(2)若AE=4,BC=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com