
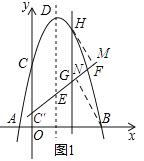
����Ŀ����ͼ1��ʾ����֪������![]() �Ķ���ΪD����x�ύ��A��B���㣬��y�ύ��C�㣬EΪ�Գ����ϵ�һ�㣬����CE�����߶�CE�Ƶ�E����ʱ�뷽����ת90����C�Ķ�Ӧ��C��ǡ������y���ϣ�
�Ķ���ΪD����x�ύ��A��B���㣬��y�ύ��C�㣬EΪ�Գ����ϵ�һ�㣬����CE�����߶�CE�Ƶ�E����ʱ�뷽����ת90����C�Ķ�Ӧ��C��ǡ������y���ϣ�

��1��ֱ��д��D���E������ꣻ
��2����FΪֱ��C��E����֪�����ߵ�һ�����㣬��H����������C��F֮���һ�����㣬������H��ֱ��HG��y��ƽ�У�����ֱ��C��E���ڵ�G�����H�ĺ�����Ϊm��0��m��4������ô��mΪ��ֵʱ��![]() =5��6��
=5��6��
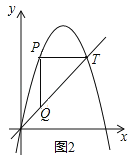
��3��ͼ2��ʾ������������![]() ����ƽ��1����λ��õ��ģ���T��5��y�����������ϣ���P����������O��T֮�������һ�㣬���߶�OT���Ƿ����һ��Q��ʹ��PQT�ǵ���ֱ�������Σ������ڣ������Q�����ꣻ�������ڣ���˵�����ɣ�
����ƽ��1����λ��õ��ģ���T��5��y�����������ϣ���P����������O��T֮�������һ�㣬���߶�OT���Ƿ����һ��Q��ʹ��PQT�ǵ���ֱ�������Σ������ڣ������Q�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��D��2��9����E��2��3������2��![]() ��
��![]() ����3����1��1����3��3����2��2����
����3����1��1����3��3����2��2����
��������
���⣨1�����������䷽�����ɵõ�����ΪD�����꣬Ȼ�����E�������ǣ�2��m������C���������ǣ�0��n����������CEC���ǵ���ֱ�������Σ����E������ꣻ
��2���������ߵ�y=0�������A��B�����꣬Ȼ���ٸ���![]() =5��6���õ���
=5��6���õ���![]() ��Ȼ����֤����HGM�ס�ABN��
��Ȼ����֤����HGM�ס�ABN��![]() ���Ӷ���֤��
���Ӷ���֤��![]() ������HG=5�����H��m����m2+4m+5����G��m��m+1����������HG=5���г�����m�ķ�����⼴�ɣ�
������HG=5�����H��m����m2+4m+5����G��m��m+1����������HG=5���г�����m�ķ�����⼴�ɣ�
��3���ֱ������P����Q����TΪֱ�ǻ���ͼ�Σ�Ȼ�����õ���ֱ�������ε����ʺ�һ�κ�����ͼ���������õ�Q�����꼴�ɣ�
�����������1����������![]() =
=![]() ����D��������ǣ�2��9������EΪ�Գ����ϵ�һ�㣬����E�ĺ�������2�����E�������ǣ�2��m������C���������ǣ�0��n���������߶�CE�Ƶ�E����ʱ�뷽����ת90����C�Ķ�Ӧ��C��ǡ������y���ϣ����CEC���ǵ���ֱ�������Σ���
����D��������ǣ�2��9������EΪ�Գ����ϵ�һ�㣬����E�ĺ�������2�����E�������ǣ�2��m������C���������ǣ�0��n���������߶�CE�Ƶ�E����ʱ�뷽����ת90����C�Ķ�Ӧ��C��ǡ������y���ϣ����CEC���ǵ���ֱ�������Σ���![]() ����ã�
����ã�![]() ��
��![]() ����ȥ��������E�������ǣ�2��3������C���������ǣ�0��1����
����ȥ��������E�������ǣ�2��3������C���������ǣ�0��1����
���ϣ��ɵ�D��������ǣ�2��9������E�������ǣ�2��3����
��2����ͼ1��ʾ��
��������![]() ��y=0�ã�
��y=0�ã�![]() ����ã�
����ã�![]() ��
��![]() �����Ե�A����1��0����B��5��0������ֱ��C��E�Ľ���ʽ��
�����Ե�A����1��0����B��5��0������ֱ��C��E�Ľ���ʽ��![]() ����E��2��3����C����0��1���������
����E��2��3����C����0��1���������![]() ����ã�
����ã�![]() ����ֱ��C��E�Ľ���ʽΪ
����ֱ��C��E�Ľ���ʽΪ![]() �������ã�
�������ã�![]() ����ã�
����ã�![]() ����
����![]() ������F������Ϊ��4��5������A����1��0����ֱ��C��E�ϣ���ֱ��C��E�Ľ���ʽΪ
������F������Ϊ��4��5������A����1��0����ֱ��C��E�ϣ���ֱ��C��E�Ľ���ʽΪ![]() �����FAB=45��������B��H�ֱ���BN��AF��HM��AF������ֱ�ΪN��M�����HMN=90������ADN=90�������ߡ�NAD=��HNM=45�������HGM�ס�ABN����
�����FAB=45��������B��H�ֱ���BN��AF��HM��AF������ֱ�ΪN��M�����HMN=90������ADN=90�������ߡ�NAD=��HNM=45�������HGM�ס�ABN����![]() ����
����![]() =5��6����
=5��6����![]() ����
����![]() ����
����![]() ����HG=5�����H�ĺ�����Ϊm�����H��������Ϊ
����HG=5�����H�ĺ�����Ϊm�����H��������Ϊ![]() �����G������Ϊ��m��m+1������
�����G������Ϊ��m��m+1������![]() ����ã�
����ã�![]() ��
��![]() ��
��
��3����ƽ�ƵĹ��ɿ�֪��ƽ�ƺ������ߵĽ���ʽΪ![]() =
=![]() ����x=5����
����x=5����![]() �ã�y=5������T������Ϊ��5��5������ֱ��OT�Ľ���ʽΪ
�ã�y=5������T������Ϊ��5��5������ֱ��OT�Ľ���ʽΪ![]() ����x=5��y=5����ã�k=1����ֱ��OT�Ľ���ʽΪ
����x=5��y=5����ã�k=1����ֱ��OT�Ľ���ʽΪ![]() ��
��
����ͼ2��ʾ����PT��x��ʱ����PTQΪ����ֱ�������Σ�
��y=5����������![]() �ã�
�ã�![]() ����ã�
����ã�![]() ��
��![]() ������P��������1��5������x=1����
������P������Ϊ��1��5������x=1����![]() �ã�y=1������Q������Ϊ��1��1����
�ã�y=1������Q������Ϊ��1��1����
����ͼ3��ʾ��
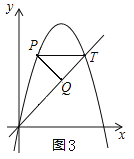
������֪����P������Ϊ��1��5�����ߡ�PTQΪ����ֱ�������Σ�����Q�ĺ�����Ϊ3����x=3����![]() �ã�y=3������Q������Ϊ��3��3����
�ã�y=3������Q������Ϊ��3��3����
����ͼ4��ʾ��
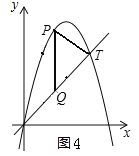
��ֱ��PT����ʽΪ![]() ����ֱ��PT��QT����k=��1����k=��1��x=5��y=5����
����ֱ��PT��QT����k=��1����k=��1��x=5��y=5����![]() �ã�b=10����ֱ��PT�Ľ���ʽΪ
�ã�b=10����ֱ��PT�Ľ���ʽΪ![]() �������ã�
�������ã�![]() ����ã�
����ã�![]() ��
��![]() ������P�ĺ�����Ϊ2����x=2����
������P�ĺ�����Ϊ2����x=2����![]() �ã�y=2������Q������Ϊ��2��2����
�ã�y=2������Q������Ϊ��2��2����
������������Q��������1��1����3��3����2��2����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
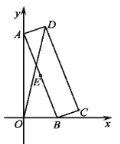
����Ŀ����ͼ������ӲֽƬABCD�Ķ���A��![]() ��������ἰԭ���ϻ���������B��
��������ἰԭ���ϻ���������B��![]() ��������ἰԭ���ϻ�������EΪAB���е㣬AB=24,BC=5,�������н��ۣ��ٵ�A�ӵ�O����������B�˶�����OΪֹ����E������·����Ϊ12��������OAB����������ֵΪ144���۵�OD���ʱ����D������Ϊ
��������ἰԭ���ϻ�������EΪAB���е㣬AB=24,BC=5,�������н��ۣ��ٵ�A�ӵ�O����������B�˶�����OΪֹ����E������·����Ϊ12��������OAB����������ֵΪ144���۵�OD���ʱ����D������Ϊ![]() ��������ȷ�Ľ�����_________����д��ţ�.
��������ȷ�Ľ�����_________����д��ţ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
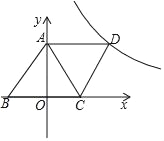
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��ı���ABCD�����Σ���A��0��4����B����3��0������������y=![]() ��kΪ������k��0��x��0����ͼ����D��
��kΪ������k��0��x��0����ͼ����D��
��1����գ�k=_____��
��2����֪��y=![]() ��ͼ������һ��N��y������һ��M�����ı���ABMN��ƽ���ı��Σ����M�����꣮
��ͼ������һ��N��y������һ��M�����ı���ABMN��ƽ���ı��Σ����M�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ij��������ɫ���С���ʽ�������ijУ��ѧ��ȤС�����ʾ��������ʽ�����������ij�в��ֳ����������Ҫ���з�ʽ�������ʾ����������ֻ���������������ѡ��һ�ࣩ���������������Ƴ����²�������ͳ��ͼ��
���� | A | B | C | D | E |
���з�ʽ | �������� | ���� | ������ | ��ʿ | ˽�ҳ� |

����������Ϣ���ش��������⣺
��1�����뱾���ʾ������������ �ˣ�����ѡ��B��������� �ˣ�
��2��������ͳ��ͼ�У���A���Ӧ����Բ�ĽǦ��Ķ���������ȫ����ͳ��ͼ��
��3������Լ��12���˳��У�����A��B��C��������з�ʽ����Ϊ����ɫ���С���ʽ������Ƹ��С���ɫ���С���ʽ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ó��˾����ij��ˮ���ijɱ�Ϊ20Ԫ/kg�������г����з��֣�����ˮ����δ��48������۵���p��Ԫ/kg����ʱ��t���죩֮��ĺ�����ϵʽΪ��
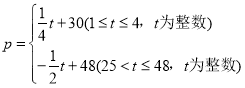 ��������������y��kg����ʱ��t���죩�Ĺ�ϵ���±���
��������������y��kg����ʱ��t���죩�Ĺ�ϵ���±���

��1����֪y��t֮��ı仯���ɷ���һ�κ�����ϵ�������ڵ�30������������Ƕ��٣�
��2������һ���������������������������Ϊ���٣�
��3����ʵ�����۵�ǰ24���У���˾����ÿ����1kgˮ���;���nԪ����n��9����������ƶ�������ַ��֣���ǰ24���У�ÿ��۳��������������������ʱ��t�������������n��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
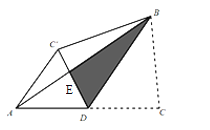
����Ŀ����ͼ���ڡ�ABC�У�D��AC���ϵ��е㣬����BD���ѡ�BDC����BD���ۣ��õ���![]() ��DC��AB���ڵ�E������
��DC��AB���ڵ�E������![]() ����AD=AC��=2��BD=3���D��BC�ľ���Ϊ�� ��
����AD=AC��=2��BD=3���D��BC�ľ���Ϊ�� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ڽ�����ϵ�У�������y=x2-2x-3��x�ύ���A��B����A�ڵ�B����ࣩ��y���ڵ�C����DΪ�����ߵĶ��㣬�Գ�����x�ύ�ڵ�E��
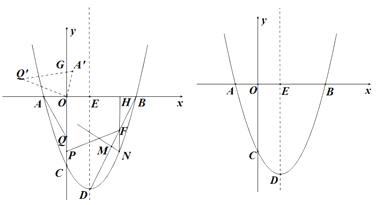
��1������BD����M���߶�BD��һ���㣨��M����˵�B��D�غϣ�������M��MN��BD���������ڵ�N����N�ڶԳ�����Ҳࣩ������N��NH��x�ᣬ����ΪH����BD�ڵ�F����P���߶�OC��һ���㣬��MNȡ�����ֵʱ����HF+FP+![]() PC����Сֵ��
PC����Сֵ��
��2���ڣ�1���У���MNȡ�����ֵHF+FP+1/3PCȡ��Сֵʱ���ѵ�P����ƽ�Ƹ�![]() ��λ�õ���Q������AQ���ѡ�AOQ�Ƶ�Oƿʱ����תһ���ĽǶ�
��λ�õ���Q������AQ���ѡ�AOQ�Ƶ�Oƿʱ����תһ���ĽǶ�![]() ��0��<
��0��<![]() <360�㣩���õ���AOQ�����б�AQ���������ڵ�C����ת�����У��Ƿ����һ��Gʹ��
<360�㣩���õ���AOQ�����б�AQ���������ڵ�C����ת�����У��Ƿ����һ��Gʹ��![]() �������ڣ���ֱ��д���������������ĵ�Q�����ꣻ�������ڣ���˵�����ɣ�
�������ڣ���ֱ��д���������������ĵ�Q�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
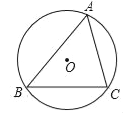
����Ŀ����ͼ����ABC�ڽ�����O��
��1������B��ƽ��������O���ڵ�D���ó߹���ͼ������д��������Ҫ������ͼ�ۼ�����
��2���ڣ�1����������AD������BAC=60������C=66��������DAC�Ĵ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ƽ��ֱ������ϵxOy�еĶ���P��ͼ��N���������¶��壺���QΪͼ��N��һ�����㣬P��Q������������ֵΪdmax��P��Q�����������СֵΪdmin�����ǰ�dmax+dmin��ֵ�е�P��ͼ��N������;�����������d��P��ͼ��N����
��1����ͼ1��������ABCD������Ϊ��O��A��3��3����
�ٵ�O���߶�AB�����;�����d��O���߶�AB��=______��
�������������y�ύ�ڵ�E��F����P���߶�EF�ϣ�d��P��������ABCD��=7�����P�����꣮
��2����ͼ2���ڣ�1���������£���C��D����������CD������AC����M������CD�ϵ�һ�����㣬���6![]() ��d��M���߶�AC����6+3
��d��M���߶�AC����6+3![]() ��ֱ��д��M�������tȡֵ��Χ��
��ֱ��д��M�������tȡֵ��Χ��
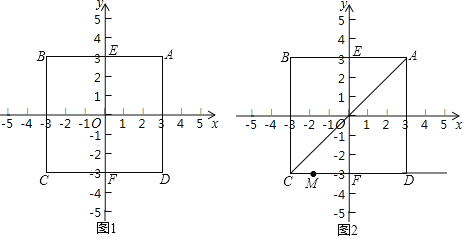
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com