
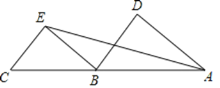
【题目】已知A,B,C三点在同一直线上,∠DAE=∠AEB,∠D=∠BEC,
(1)求证:BD∥CE;
(2)若∠C=70°,∠DAC=50°,求∠DBE的度数.
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.

(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个多边形的各边都相等且各角也都相等,那么这样的多边形叫做正多边形,如正三角形就是等边三角形,正四边形就是正方形,如下图,就是一组正多边形,

(1)观察上面每个正多边形中的∠α,填写下表:
正多边形边数 | 3 | 4 | 5 | 6 | …… | n |
∠α的度数 | ______° | _____° | ______° | ______° | …… | _____° |
(2)根据规律,计算正八边形中的∠α的度数.
(3)是否存在正n边形使得∠α=21°?若存在,请求出n的值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:探究函数的图象与性质.
小华根据学习函数的经验,对函数的图象与性质进行了探究.下面是小华的探究过程,请补充完整:
在函数![]() 中,自变量
中,自变量![]() 可以是任意实数;
可以是任意实数;
(1)下表是![]() 与
与![]() 的几组对应值.
的几组对应值.
| … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
| … | 1 | 0 | -1 | -2 | -1 | 0 |
| … |
①![]() ______;
______;
②若![]() ,
,![]() 为该函数图象上不同的两点,则
为该函数图象上不同的两点,则![]() ______;
______;
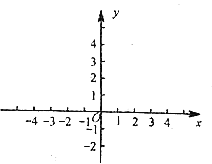
(2)如图,在平面直角坐标系![]() 中,描出以上表中各对对应值为坐标的点.并根据描出的点,画出该函数的图象;
中,描出以上表中各对对应值为坐标的点.并根据描出的点,画出该函数的图象;
(3)根据函数图象可得函数的性质:
①该函数的最小值为______;
②再写出该函数一条性质____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
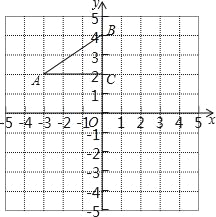
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2;请在图中标明旋转中心P的位置并写出其坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课的变化而变化,开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如图所示(其中AB、BC分别为线段,CD为双曲线的一部分):
(1)开始上课后第五分钟时与第三十分钟时相比较,何时学生的注意力更集中?
(2)一道数学竞赛题,需要讲16分钟,为了效果较好,要求学生的注意力指标数最低达到36,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小易同学在数学学习时,遇到这样一个问题:如图,已知点![]() 在直线
在直线![]() 外,请用一把刻度尺(仅用于测量长度和画直线),画出过点
外,请用一把刻度尺(仅用于测量长度和画直线),画出过点![]() 且平行于
且平行于![]() 的直线,并简要说明你的画图依据.
的直线,并简要说明你的画图依据.

小易想到一种作法:
①在直线![]() 上任取两点
上任取两点![]() 、
、![]() (两点不重合);
(两点不重合);
②利用刻度尺连接![]() 并延长到
并延长到![]() ,使
,使![]() ;
;
③连接![]() 并量出
并量出![]() 中点
中点![]() ;
;
④作直线![]() .
.
∴直线![]() 即为直线
即为直线![]() 的平行线.
的平行线.

(1)请依据小易同学的作法,补全图形.
(2)证明:∵![]() ,
,
∴![]() 为
为![]() 的中点,
的中点,
又∵![]() 为
为![]() 中点,
中点,
∴![]() ( )
( )
(3)你还有其他画法吗?请画出图形,并简述作法.
作法:

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题解决:如图1,![]() 中,
中,![]() 为
为![]() 边上的中线,则
边上的中线,则![]() ______
______![]() .
.
问题探究:
(1)如图2,![]() 分别是
分别是![]() 的中线,
的中线,![]() 与
与![]() 相等吗?
相等吗?
解:![]() 中,由问题解决的结论可得,
中,由问题解决的结论可得,![]() ,
,![]() .
.
∴![]()
∴![]()
即![]() .
.
(2)图2中,仿照(1)的方法,试说明![]() .
.
(3)如图3,![]() ,
,![]() ,
,![]() 分别是
分别是![]() 的中线,则
的中线,则![]() ______
______![]() ,
,![]() ______
______![]() ,
,![]() ______
______![]() .
.

问题拓展:
(1)如图4,![]() 分别为四边形
分别为四边形![]() 的边
的边![]() 的中点,请直接写出阴影部分的面积与四边形
的中点,请直接写出阴影部分的面积与四边形![]() 的面积之间的数量关系:
的面积之间的数量关系:![]() ______
______![]() .
.

(2)如图5,![]() 分别为四边形
分别为四边形![]() 的边
的边![]() 的中点;请直接写出阴影部分的面积与四边形
的中点;请直接写出阴影部分的面积与四边形![]() 的面积之间的数量关系:
的面积之间的数量关系:![]() ______
______![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】去冬今春,我市部分地区遭受了罕见的旱灾,“旱灾无情人有情”.某单位给某乡中小学捐献一批饮用水和蔬菜共320件,其中饮用水比蔬菜多80件.
(1)求饮用水和蔬菜各有多少件?
(2)现计划租用甲、乙两种货车共8辆,一次性将这批饮用水和蔬菜全部运往该乡中小学.已知每辆甲种货车最多可装饮用水40件和蔬菜10件,每辆乙种货车最多可装饮用水和蔬菜各20件.则运输部门安排甲、乙两种货车时有几种方案?请你帮助设计出来;
(3)在(2)的条件下,如果甲种货车每辆需付运费400元,乙种货车每辆需付运费360元.运输部门应选择哪种方案可使运费最少?最少运费是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com