
����Ŀ������������ͼ1��![]() �У�
�У�![]() Ϊ
Ϊ![]() ���ϵ����ߣ���
���ϵ����ߣ���![]() ______
______![]() .
.
����̽����
��1����ͼ2��![]() �ֱ���
�ֱ���![]() �����ߣ�
�����ߣ�![]() ��
��![]() �����
�����
�⣺![]() �У����������Ľ��ۿɵã�
�У����������Ľ��ۿɵã�![]() ��
��![]() .
.
��![]()
��![]()
��![]() .
.
��2��ͼ2�У����գ�1���ķ�������˵��![]() .
.
��3����ͼ3��![]() ��
��![]() ��
��![]() �ֱ���
�ֱ���![]() �����ߣ���
�����ߣ���![]() ______
______![]() ��
��![]() ______
______![]() ��
��![]() ______
______![]() .
.

������չ��
��1����ͼ4��![]() �ֱ�Ϊ�ı���
�ֱ�Ϊ�ı���![]() �ı�
�ı�![]() ���е㣬��ֱ��д����Ӱ���ֵ�������ı���
���е㣬��ֱ��д����Ӱ���ֵ�������ı���![]() �����֮���������ϵ��
�����֮���������ϵ��![]() ______
______![]() .
.

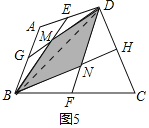
��2����ͼ5��![]() �ֱ�Ϊ�ı���
�ֱ�Ϊ�ı���![]() �ı�
�ı�![]() ���е㣻��ֱ��д����Ӱ���ֵ�������ı���
���е㣻��ֱ��д����Ӱ���ֵ�������ı���![]() �����֮���������ϵ��
�����֮���������ϵ��![]() ______
______![]() .
.
���𰸡�����������1��![]() ��2������������3��
��2������������3��![]() ��
��![]() ��
��![]() ��
��
������չ����1��![]() ����2��
����2��![]() ��
��
��������
����������1����������ƽ�����������⣻
��2������![]() ���ֱ��ȥ��BOC�����������⣻
���ֱ��ȥ��BOC�����������⣻
��3���������ߵ����ʵõ���С�����ε��������ȣ�������⣻
������չ����1������BD��������������1���Ľ��ۼ�����⣻
��2������BD��������������2���Ľ��ۼ������.
����������1����![]() ��
�У�![]() Ϊ
Ϊ![]() ���ϵ����ߣ�
���ϵ����ߣ�
��![]()
![]()
![]() .
.
��2���⣺![]() �У����������Ľ��ۿɵã�
�У����������Ľ��ۿɵã�![]() ��
��![]() .
.
��![]()
��![]()
��![]() .
.
��3����![]() ��
��![]() ��
��![]() �ֱ���
�ֱ���![]() �����ߣ�
�����ߣ�
�ɣ�2���ɵ�![]()
��![]()
![]()
![]() ��
��![]()
![]()
![]() ��
��![]()
![]()
![]() .
.
������չ����1����ͼ������BD������������1���Ľ��۵�![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,
��![]()
![]()
![]()
![]()
![]()

��2����ͼ����BD��������������2���Ľ��۵�
![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,
��![]()
![]()
![]()
![]()
![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC����������ֱ�ΪA��2��3����B��3��1����C����2����2����

��1������ͼ��������ABC����y�����Գ�ͼ�Ρ�DEF��A��B��C�Ķ�Ӧ��ֱ���D��E��F������ֱд��D��E��F�����꣮
��2�����ı���ABED�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
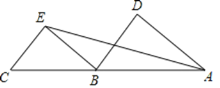
����Ŀ����֪A��B��C������ͬһֱ���ϣ���DAE=��AEB����D=��BEC��
��1����֤��BD��CE��
��2������C=70������DAC=50��������DBE�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����A��B���鿨Ƭ��5�ţ�A������ŷֱ�д������2��4��6��B������ŷֱ�д��3��5�����dz���������û���κ�������
��1�������A���ȡһ�ţ���鵽����Ϊ2�ĸ��ʣ�
��2������طֱ��A�顢B�����ȡһ�ţ��������б�����״ͼ�ķ�����ʾ���еȿ��ܵĽ��.���ƶ�����һ����Ϸ������ѡ��������֮��Ϊ3�ı��������ʤ�������һ�ʤ��������������Ϸ����Լ���˫����ƽ��Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ijС��ʵʩ��ů���칤�̣��ּס��������̶ӷֱ�ͬʱ��������600�׳��Ĺܵ������ڹܵ�����y���ף����ھ�ʱ��x���죩֮��Ĺ�ϵ��ͼ��ʾ��������˵���У���ȷ�ĸ����У� ������
����ÿ����100�ף�
���Ҷӿ��������ÿ����50�ף�
����x=4ʱ���ס����������ڹܵ�������ͬ��
���ӱ��Ҷ���ǰ2���������

A. 1 B. 2 C. 3 D. 4
���𰸡�D
������������ÿ����![]() =100��,��ȷ.
=100��,��ȷ.
���Ҷӿ��������ÿ���ڣ� ![]() �ף���ȷ.
�ף���ȷ.
����x=4ʱ���ס������ӽ�����x=4���������ڹܵ�������ͬ.��ȷ.
������֪���������ʱ���һ���100�ף�100![]() 2. �ӱ��Ҷ���ǰ2�����������ȷ.
2. �ӱ��Ҷ���ǰ2�����������ȷ.
��ѡD.
�����͡���ѡ��
��������
11
����Ŀ��103 000�ÿ�ѧ��������ʾΪ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=AC����B=30����DΪBC��һ�㣬�ҡ�DAB=45����
(1) ���DAC�Ķ�����
(2) ��֤����ACD�ǵ��������Σ�
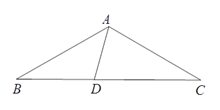
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ı���ABCD�ڽ��ڡ�O����EΪAD��һ�㣬����AC��CB����B=��AEC��
��1����ͼ1����֤��CE=CD��

��2����ͼ2������B+��CAE=120�㣬��ACD=2��BAC�����BAD�Ķ�����

��3����ͼ3���ڣ�2���������£��ӳ�CE����O�ڵ�G����tan��BAC= ![]() ��EG=2����AE�ij���
��EG=2����AE�ij���

���𰸡���1������������2��60�㣻��3��7.
�����������������(1)����Բ���ڽ��ı��ζ����õ���CED=��CDE.
(2) ��CH��DE��H, ����ECH=�����ɣ�1��CE=CD��������ʾ��CAE����BAC������BAD=��BAC+��CAE.��3������AG����GN��AC��AM��EG����֤����CAG=��BAC����NG=5![]() m���ɵ�AN=11m������ֱ��
m���ɵ�AN=11m������ֱ��![]() AGM,
AGM, ![]() AEM�����ɶ����������m��ֵ�����AE��.
AEM�����ɶ����������m��ֵ�����AE��.
���������
��1���⣺֤�������ı���ABCD�ڽ�����O.
���B+��D=180����
�ߡ�B=��AEC��
���AEC+��D=180����
�ߡ�AEC+��CED=180����
���D=��CED��
��CE=CD��
��2���⣺��CH��DE��H��

����ECH=�����ɣ�1��CE=CD��
���ECD=2����
�ߡ�B=��AEC����B+��CAE=120����
���CAE+��AEC=120����
���ACE=180�㩁��AEC����ACE=60����
���CAE=90�㩁��ACH=90�㩁��60��+����=30�㩁����
��ACD=��ACH+��HCD=60��+2����
�ߡ�ACD=2��BAC��
���BAC=30��+����
���BAD=��BAC+��CAE=30��+��+30�㩁��=60����
��3���⣺����AG����GN��AC��AM��EG��
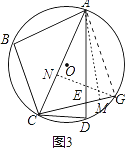
�ߡ�CED=��AEG����CDE=��AGE����CED=��CDE��
���AEG=��AGE��
��AE=AG��
��EM=MG=![]() EG=1��
EG=1��
���EAG=��ECD=2����
���CAG=��CAD+��DAG=30�㩁��+2��=��BAC��
��tan��BAC=![]() ��
��
����NG=5![]() m���ɵ�AN=11m��AG=
m���ɵ�AN=11m��AG=![]() =14m��
=14m��
�ߡ�ACG=60����
��CN=5m��AM=8![]() m��MG=
m��MG=![]() =2m=1��
=2m=1��
��m=![]() ��
��
��CE=CD=CG��EG=10m��2=3��
��AE=![]() =
=![]() =7��
=7��
�����͡������
��������
27
����Ŀ�����κ���y=��x��1��2+k�ֱ���x�ᡢy�ύ��A��B��C���㣬��A�ڵ�B����ֱ࣬��y=��![]() x+2������B������y�ύ�ڵ�D��
x+2������B������y�ύ�ڵ�D��
��1����ͼ1����k��ֵ��

��2����ͼ2���ڵ�һ��������������һ����P������AP����P��PE��x���ڵ�E����E��EF��AP�ڵ�F������D��ƽ����x���ֱ�߷ֱ���ֱ��FE��PE���ڵ�G��H�����P�ĺ�����Ϊt���߶�GH�ij�Ϊd����d��t�ĺ�����ϵʽ����ֱ��д��t��ȡֵ��Χ��

��3���ڣ�2���������£�����G��ƽ����y���ֱ�߷ֱ�AP��x����������ڵ�M��T��N��tan��MEA= ![]() ����KΪ����������������һ�㣬���ڶԳ�����࣬����KA��������KA��ȡһ��R������RM������K��KQ��AK��PE���ӳ�����Q������AQ��HK������RAE����RMA=45������AKQ���HKQ�������ȣ����R�����꣮
����KΪ����������������һ�㣬���ڶԳ�����࣬����KA��������KA��ȡһ��R������RM������K��KQ��AK��PE���ӳ�����Q������AQ��HK������RAE����RMA=45������AKQ���HKQ�������ȣ����R�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
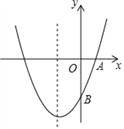
����Ŀ����ͼ����֪������y=ax2+bx+c��a��0���ĶԳ���Ϊֱ��x=��1���Ҿ�A��1��0����
B��0����3�����㣮��1���������ߵĽ���ʽ��
��2���������ߵĶԳ���x=��1�ϣ��Ƿ���ڵ�M��ʹ������A�ľ����뵽��B�ľ���֮����С��������������M�����꣬�����������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧΪ�˽���꼶ѧ������������������������˾��꼶����ѧ��һ�����������������Ƴ�����ͳ��ͼ����ͼ1��ͼ2��������
�ȼ� | һ������������x | ���� |
A | x��180 | 12 |
B | 150��x��180 | 14 |
C | 120��x��150 | a |
D | x��120 | b |

����ͼ������������⣺
��1����1��a=�� ����b=�� ����
��2�����ͼ1��ͼ2����������
��3����֪��У��1000�����꼶ѧ��������һ��������������������120�ε�Ϊ���ϸ����У���꼶ѧ��һ�����������ϸ��ѧ������Ϊ�� ���ˣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com