练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，已知△ABC的三个顶点分别为A（2，3）、B（3，1）、C（－2，－2）．

    （1）请在图中作出△ABC关于y轴的轴对称图形△DEF（A、B、C的对应点分别是D、E、F），并直写出D、E、F的坐标．

    （2）求四边形ABED的面积．

    【答案】（1）图见解析；D(-2,3)，E(-3,1)，F(2,-2) （2）10

    【解析】

    （1）首先确定A、B、C的关于y轴的对称点D、E、F的位置，再顺次连接即可，然后写出D、E、F的坐标；
    （2）根据梯形的面积公式，即可求解．

    （1）如图所示：△DEF即为所求三角形，由图形可知：D(-2，3)，E(-3，1)，F(2，-2)；

    （2）连接AD，BE，

    ∵AD∥BE，

    ∴四边形ABED是梯形，

    ∴四边形ABED的面积=．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某大型超市从生产基地购进一批水果，运输过程中质量损失10%，假设超市购进这批水果的总量为m千克，每千克进价为n元（不计超市其它费用）．

    （1）如果超市在进价的基础上提高10%作为售价，此时：

    ①超市最终的销售额为_________元（用含m、n的代数式表示）；

    ②在这一次销售中，超市_______（填：盈利或亏本）．

    （2）如果超市至少要获得17%的利润，请通过计算说明这种水果的售价最低应提高百分之几？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，AB=AC，AD是△ABC的角平分线，点O为AB的中点，连接DO并延长到点E，使OE=OD，连接AE，BE．

    （1）求证：四边形AEBD是矩形；

    （2）当△ABC满足什么条件时，矩形AEBD是正方形，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】从2开始，连续的偶数相加，它们和的情况如下表：

    加数的个数n

    S

    1

    2=1×2

    2

    2＋4=6=2×3

    3

    2＋4＋6=12=3×4

    4

    2＋4＋6＋8=20=4×5

    5

    2＋4＋6＋8＋10=30=5×6

    （1）若n=8时，则S的值为_____________．

    （2）根据表中的规律猜想：用n的式子表示S的公式为：S=2+4+6+8+…+2n=__________________．

    （3）根据上题的规律计算2+4+6+8+10+…+98+100的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

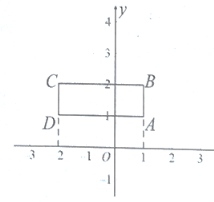
    【题目】如图，在平面直角坐标系 中，长方形 的四个顶点分别为 .对该长方形及其内部的每一个点都进行如下操作：把每个点的横坐标都乘以同一个实数 ，纵坐标都乘以3，再将得到的点向右平移 （ 同一个实数，纵坐标都乘以3，再将得到的点向右平移 个单位，向下平移2个单位，得到长方形 及其内部的点，其中点 的对应点分别为部的点.

    （1）点的横坐标为（用含，的式子表示）；

    （2）点的坐标为 ，点的坐标为 ，

    ①求，的值；

    ②若对长方形内部（不包括边界）的点 进行上述操作后，得到的对应点 仍然在长方形内部（不包括边界），求少的取值范围.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，点D为BC边的任意一点，以点D为顶点的∠EDF的两边分别与边AB，AC交于点E、F，且∠EDF与∠A互补．

    （1）如图1，若AB=AC，D为BC的中点时，则线段DE与DF有何数量关系？请直接写出结论；

    （2）如图2，若AB=kAC，D为BC的中点时，那么（1）中的结论是否还成立？若成立，请给出证明；若不成立，请写出DE与DF的关系并说明理由；

    （3）如图3，若=a，且=b，直接写出=　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如果一个多边形的各边都相等且各角也都相等，那么这样的多边形叫做正多边形，如正三角形就是等边三角形，正四边形就是正方形，如下图，就是一组正多边形，

    (1)观察上面每个正多边形中的∠α，填写下表：

    正多边形边数

    3

    4

    5

    6

    ……

    n

    ∠α的度数

    ______°

    _____°

    ______°

    ______°

    ……

    _____°

    (2)根据规律，计算正八边形中的∠α的度数.

    (3)是否存在正n边形使得∠α=21°？若存在，请求出n的值，若不存在，请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】问题：探究函数的图象与性质．

    小华根据学习函数的经验，对函数的图象与性质进行了探究．下面是小华的探究过程，请补充完整：

    在函数中，自变量可以是任意实数；

    （1）下表是与的几组对应值．

    …

    -3

    -2

    -1

    0

    1

    2

    3

    …

    …

    1

    0

    -1

    -2

    -1

    0

    …

    ①______；

    ②若，为该函数图象上不同的两点，则______；

    （2）如图，在平面直角坐标系中，描出以上表中各对对应值为坐标的点．并根据描出的点，画出该函数的图象；

    （3）根据函数图象可得函数的性质：

    ①该函数的最小值为______；

    ②再写出该函数一条性质____________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】问题解决：如图1，中，为边上的中线，则______.

    问题探究：

    （1）如图2，分别是的中线，与相等吗？

    解：中，由问题解决的结论可得，，.

    ∴

    ∴

    即.

    （2）图2中，仿照（1）的方法，试说明.

    （3）如图3，，，分别是的中线，则______，______，______.

    问题拓展：

    （1）如图4，分别为四边形的边的中点，请直接写出阴影部分的面积与四边形的面积之间的数量关系：______.

    （2）如图5，分别为四边形的边的中点；请直接写出阴影部分的面积与四边形的面积之间的数量关系：______.

    查看答案和解析>>

    同步练习册答案