
【题目】如图是单位长度为1的正方形网格,若A,B两点的坐标分别为![]() ,
,![]() .
.
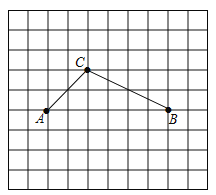
请解决下列问题:
(1)在网格图中画出平面直角坐标系,并直接写出点C的坐标_________.
(2)将图中三角形ABC沿x轴向右平移1个单位,再沿y轴向上平移2个单位后得到三角形![]() ,则
,则![]() 的坐标为_________;
的坐标为_________;![]() 的坐标为_________;
的坐标为_________;![]() 的坐标为_________;
的坐标为_________;
(3)在y轴上是否存在点P,使得三角形![]() 的面积为4,若存在,请直接写出P点坐标:若不存在,请说明理由.
的面积为4,若存在,请直接写出P点坐标:若不存在,请说明理由.
【答案】(1)图略, ![]() ;(2)
;(2)![]() ,
,![]() ,
,![]() ;(3)存在,
;(3)存在,![]()
![]() .
.
【解析】
(1)利用A、B点的坐标建立平面直角坐标系,然后写出点C的坐标;
(2)利用点平移的坐标变换规律分别写出点A1、B1、C1的坐标,然后描点即可;
(3)设P(0,t),根据三角形面积公式得到![]() 2×|t﹣6|=4,然后解绝对值方程求出t,从而得到P点坐标.
2×|t﹣6|=4,然后解绝对值方程求出t,从而得到P点坐标.
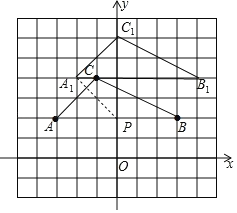
(1)如图,C点坐标为(﹣1,4);
(2)如图,△A1B1C1为所作;A1的坐标为(﹣2,4);B1的坐标为(4,4);C1的坐标为(0,6).
故答案为:(﹣1,4),(﹣2,4),(4,4),(0,6);
(3)存在.
设P(0,t),根据题意得:![]() 2×|t﹣6|=4,解得:t=2或t=10,所以满足条件的P点坐标为(0,2)或(0,10).
2×|t﹣6|=4,解得:t=2或t=10,所以满足条件的P点坐标为(0,2)或(0,10).


科目:初中数学 来源: 题型:
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
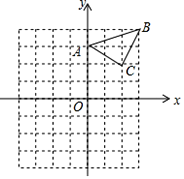
(1)△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 ;(画出图形)
(3)△A2B2C2的面积是 平方单位.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,四边形ABCD是平行四边形,AC、BD交于点O,∠1=∠2.
(1)求证:四边形ABCD是矩形;(2)若∠BOC=120°,AB=4cm,求四边形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边型ABCD中,AB∥DC,过对角线AC的中点O作![]() ,分别交边AB,CD于点E,F,连接CE,AF.
,分别交边AB,CD于点E,F,连接CE,AF.

(1)求证:四边形AECF是菱形;
(2)若EF=8,AE=5,求四边形AECF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
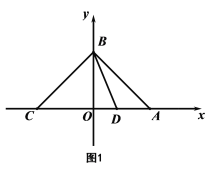
【题目】如图,在平面直角坐标系xOy中,A(a,0),B(0,b),C(-a,0),且![]() +b2-4b+4=0.
+b2-4b+4=0.
(1)求证:∠ABC=90°;
(2)∠ABO的平分线交x轴于点D,求D点的坐标.
(3)如图,在线段AB上有两动点M、N满足∠MON=45°,求证:BM2+AN2=MN2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在Rt△ABC中,∠BAC=90°,AD是斜边BC上的高,BE为∠ABC的角平分线交AC于E,交AD于F,FG∥BD,交AC于G,过E作EH⊥CD于H,连接FH,下列结论:①四边形CHFG是平行四边形,②AE=CG,③FE=FD,④四边形AFHE是菱形,其中正确的是( )
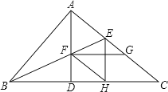
A.①②③④ B.②③④ C.①③④ D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“一带一路”国际合作高峰论坛期间,我国同30多个国家签署经贸合作协议.某工厂准备生产甲、乙两种商品共6万件销往“一带一路”沿线国家和地区,已知2件甲种商品与3件乙种商品的销售收入相同,3件甲种商品比2件乙种商品的销售收入多1500元.
(1)甲种商品与乙种商品的销售单价各多少元?
(2)若甲、乙两种商品的销售总收入不低于4200万元,则至少销管甲种商品多少万件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,∠ACD=30°,BD=6,
求(1)∠BAD,∠ABC的度数;
(2)求AB,AC的长;
(3)求菱形ABCD的面积。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(三角形顶点是网格线的交点)和△A1B1C1,且△ABC与△A1B1C1,成中心对称.
(1)画出△ABC和△A1B1C1的对称中心![]() ;
;
(2)将△A1B1C1沿直线![]() 方向向上平移6格,得到△A2B2C2,画出△A2B2C2;
方向向上平移6格,得到△A2B2C2,画出△A2B2C2;
(3)将△A2B2C2绕点C2顺时针方向旋转90°,得到△A3B3C3,画出△A3B3C3.
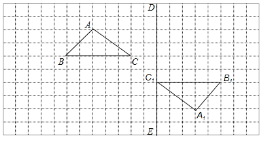
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com