
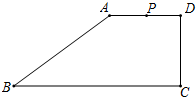
 已知在梯形ABCD中,AD∥BC,∠ADC=90°,且AD=DC=3cm,AB=5cm,动点P从A点出发,以1cm/s的速度沿折线A-D-C运动,过点P作PQ∥AB,交BC于点Q,设运动时间为t(s),
已知在梯形ABCD中,AD∥BC,∠ADC=90°,且AD=DC=3cm,AB=5cm,动点P从A点出发,以1cm/s的速度沿折线A-D-C运动,过点P作PQ∥AB,交BC于点Q,设运动时间为t(s),分析 (1)由ASA即可证明△CPQ≌△DPE;
(2)分两种情形:
情形1:当P2A⊥Q2A时,证明△ABO∽△P2Q2C,得出Q2C=$\frac{4}{3}$(6-t),再证明△ADP2≌△AOQ2,得出DP2=OQ2,列出方程$\frac{4}{3}$(6-t)-3=t-3,解方程即可;
情形2:当AQ11⊥P1Q1时,根据射影定理求出OQ1=$\frac{9}{4}$,得出CQ13=$\frac{3}{4}$,再证明△ABO∽△P1Q1C,求出P1C=$\frac{9}{16}$,即可得出t=6-$\frac{9}{16}$=$\frac{87}{16}$.
解答 (1)证明:如图1所示: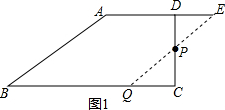 ∵点P是CD的中点,
∵点P是CD的中点,
∴DP=CP,
∵AD∥BC,∠ADC=90°,
∴∠C=90°,
在△DPE和△CPQ中,
$\left\{\begin{array}{l}{∠EDP=∠C}\\{DP=PC}\\{∠DPE=∠CPQ}\end{array}\right.$,
∴△DPE≌△CPQ(ASA);
(2)解:如图2,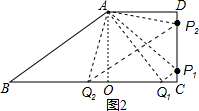 过点A作AO⊥BC于点O,
过点A作AO⊥BC于点O,
∵∠AOC=∠C=∠D=90°AD=CD=3cm,
∴四边形AOCD是正方形,
∵AB=5cm,AO=3cm,
∴BO=4cm,
情形1:当P2A⊥Q2A时,
∵AB∥P2Q2,
∴∠ABO=∠P2Q2C,
又∵∠AOPB=∠C=90°,
∴△ABO∽△P2Q2C,
∴$\frac{{P}_{2}C}{AO}$=$\frac{{Q}_{2}C}{BO}$,
则$\frac{6-t}{3}$=$\frac{{Q}_{2}C}{4}$,
∴Q2C=$\frac{4}{3}$(6-t),
在△ADP2和△AOQ2中,
$\left\{\begin{array}{l}{∠D=∠AO{Q}_{2}}\\{AD=AO}\\{∠DA{P}_{2}=∠OA{Q}_{2}}\end{array}\right.$,
∴△ADP2≌△AOQ2(ASA),
∴DP2=OQ2,
∴$\frac{4}{3}$(6-t)-3=t-3,
解得:t=$\frac{24}{7}$;
情形2:当AQ11⊥P1Q1时,
∵AO⊥BC,根据射影定理得:AO2=BO•OQ1,
∴OQ1=$\frac{{3}^{2}}{4}$=$\frac{9}{4}$,
∴CQ13=3-$\frac{9}{4}$=$\frac{3}{4}$,
∵P1Q1∥AB,
∴∠B=∠P1Q1,∠AOB=∠C=90°,
∴△ABO∽△P1Q1C,
∴$\frac{{P}_{1}C}{AO}=\frac{C{Q}_{1}}{BO}$,
∴P1C=$\frac{9}{16}$,
∴t=6-$\frac{9}{16}$=$\frac{87}{16}$,
综上所述:当△APQ为直角三角形时,t的值为$\frac{24}{7}$或$\frac{87}{16}$.
点评 本题考查了梯形的性质、全等三角形的判定与性质、相似三角形的判定与性质;本题难度较大,特别是(2)中,需要进行分类讨论,通过证明三角形全等和三角形相似才能得出答案.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
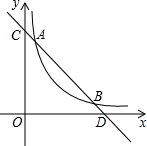 如图,已知直线y=4-x与反比例函数y=$\frac{m}{x}$(m>0,x>0)的图象交于A、B两点,与x轴、y轴分别交于C、D两点.
如图,已知直线y=4-x与反比例函数y=$\frac{m}{x}$(m>0,x>0)的图象交于A、B两点,与x轴、y轴分别交于C、D两点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com