
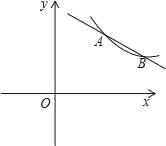
【题目】如图,点A(m,m+1),B(m+3,m﹣1)是反比例函数![]() (x>0)与一次函数y=ax+b的交点.
(x>0)与一次函数y=ax+b的交点.
求:(1)反比例函数与一次函数的解析式;
(2)根据图象直接写出当反比例函数的函数值大于一次函数的函数值时x的取值范围.
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:
【题目】水是人类的生命之源,为了鼓励居民节约用水,相关部门实行居民生活用水阶梯式计量水价政策,下表是昆明市居民“一表一户”生活用水阶梯式计费价格表的部分信息,请解答:
自来水销售价格 | |
每户每月用水量 | 单位:元/吨 |
15吨及以下 | a |
超过15吨但不超过25吨的部分 | b |
超过25吨的部分 | 5 |
(1)小王家今年3月份用水22吨,要交水费 元(用含a,b的代数式表示);
(2)小王家今年4月份用水21吨,交水费48元;邻居小李家4月份用水27吨,交水费70元,求a,b的值;
(3)如果小王家5月份用水水费计划不超过67元,则小王家5月份最多可用水多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了锻炼学生身体素质,训练定向越野技能,某校在一公园内举行定向越野挑战赛.路线图如图![]() 所示,点
所示,点![]() 为矩形
为矩形![]() 边
边![]() 的中点,在矩形
的中点,在矩形![]() 的四个顶点处都有定位仪,可监测运动员的越野进程,其中一位运动员
的四个顶点处都有定位仪,可监测运动员的越野进程,其中一位运动员![]() 从点
从点![]() 出发,沿着
出发,沿着![]() 的路线匀速行进,到达点
的路线匀速行进,到达点![]() .设运动员
.设运动员![]() 的运动时间为
的运动时间为![]() ,到监测点的距离为
,到监测点的距离为![]() .现有
.现有![]() 与
与![]() 的函数关系的图象大致如图
的函数关系的图象大致如图![]() 所示,则这一信息的来源是( ).
所示,则这一信息的来源是( ).
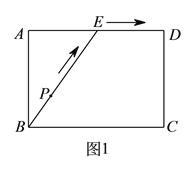

A. 监测点![]() B. 监测点
B. 监测点![]() C. 监测点
C. 监测点![]() D. 监测点
D. 监测点![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】电动自行车已成为市民日常出行的首选工具。据某市品牌电动自行车经销商1至3月份统计,该品牌电动自行车1月份销售150辆,3月销售216辆.
(1)求该品牌电动车销售量的月平均增长率;
(2)若该品牌电动自行车的进价为2300元,售价2800元,则该经销商1月至3月共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
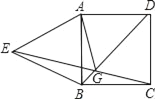
【题目】如图所示,在正方形ABCD中,以AB为边向正方形外作等边三角形ABE,连接CE、BD交于点G,连接AG,那么∠AGD的底数是______度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=![]() 与x轴交于A、B两点,△ABC为等边三角形,∠COD=60°,且OD=OC.
与x轴交于A、B两点,△ABC为等边三角形,∠COD=60°,且OD=OC.
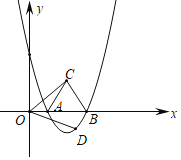
(1)A点坐标为 ,B点坐标为 ;
(2)求证:点D在抛物线上;
(3)点M在抛物线的对称轴上,点N在抛物线上,若以M、N、O、D为顶点的四边形为平行四边形,请直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣2x2+8x﹣6与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D.若直线y=x+m与C1、C2共有3个不同的交点,则m的取值范围是____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx﹣a+b(a,b为常数,且α≠0).
(1)当a=﹣1,b=1时,求顶点坐标;
(2)求证:无论a,b取任意实数,此抛物线必经过一个定点,并求出此定点;
(3)若a<0,当抛物线的顶点在最低位置时:
①求a与b满足的关系式;
②抛物线上有两点(2,s),(m,t),当s<t时,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,无人机在空中C处测得地面A、B两点的俯角分别为60°、45°,如果无人机距地面高度CD为![]() 米,点A、D、E在同一水平直线上,则A、B两点间的距离是_____米.(结果保留根号)
米,点A、D、E在同一水平直线上,则A、B两点间的距离是_____米.(结果保留根号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com