
【题目】已知抛物线y=ax2+bx﹣a+b(a,b为常数,且α≠0).
(1)当a=﹣1,b=1时,求顶点坐标;
(2)求证:无论a,b取任意实数,此抛物线必经过一个定点,并求出此定点;
(3)若a<0,当抛物线的顶点在最低位置时:
①求a与b满足的关系式;
②抛物线上有两点(2,s),(m,t),当s<t时,求m的取值范围.
【答案】(1)顶点坐标是(![]() ,
,![]() );(2)证明见解析,(﹣1,0);(3)①b=2a;②﹣4<m<2
);(2)证明见解析,(﹣1,0);(3)①b=2a;②﹣4<m<2
【解析】
(1)代入a与b的值,确定函数解析式即可求顶点坐标;
(2)将表达式因式分解,可得到当x=-1时,y=0时是函数过的顶点;
(3)由抛物线开口向下,当抛物线的顶点在最低位置时即是顶点是(-1,0)时,可求a、b关系;结合函数图象即可求m的范围.
(1)当a=﹣1,b=1时,
∴y=﹣x2+x+2=![]() ,
,
∴顶点坐标是(![]() ,
,![]() );
);
(2)y=ax2+bx﹣a+b=(ax2﹣a)+(bx+b)=a(x+1)(x﹣1)+b(x+1)=(x+1)(ax﹣a+b),
当x=﹣1时,y=0,
所以抛物线必经过定点(﹣1,0);
(3)①∵抛物线必经过定点(﹣1,0),
∴当a<0,抛物线的顶点在最低位置时,即(﹣1,0)是抛物线的顶点,
此时﹣![]() =﹣1,
=﹣1,
∴b=2a;
②当两点(2,s),(m,t),在x=﹣1右侧时:
∵s<t,
∴﹣1<m<2,
当(m,t),在x=﹣1左侧时:
∵s<t,
∴﹣4<m<﹣1,
综上所述,﹣4<m<2时,s<t.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】近年来,雾霾天气给人们的生活带来很大影响,空气质量问题倍受人们关注,某学校计划在教室内安装空气净化装置,需购进A、B两种设备,已知:购买1台A种设备和2台B种设备需要3.5万元;购买2台A种设备和1台B种设备需要2.5万元.
(1)求每台A种、B种设备各多少万元?
(2)根据学校实际,需购进A种和B种设备共30台,总费用不超过30万元,请你通过计算,求至少购买A种设备多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
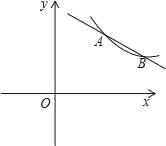
【题目】如图,点A(m,m+1),B(m+3,m﹣1)是反比例函数![]() (x>0)与一次函数y=ax+b的交点.
(x>0)与一次函数y=ax+b的交点.
求:(1)反比例函数与一次函数的解析式;
(2)根据图象直接写出当反比例函数的函数值大于一次函数的函数值时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了增强学生体质,某校对学生设置了体操、球类、跑步、游泳等课外体育活动,为了了解学生对这些项目的喜爱情况,在全校范围内随机抽取了若干名学生,对他们最喜爱的体育项目(每人只选一项)进行了问卷调查,将数据进行了统计并绘制成了如图所示的频数分布直方图和扇形统计图(均不完整).
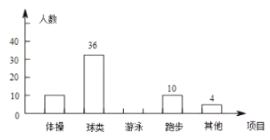
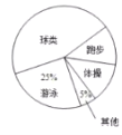
(1)在这次问卷调查中,一共抽查了多少名学生?
(2)补全频数分布直方图,求出扇形统计图中“体操”所对应的圆心角度数;
(3)估计该校![]() 名学生中有多少人喜爱跑步项目.
名学生中有多少人喜爱跑步项目.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把平面内一条数轴x绕点O逆时针旋转角θ(0°<θ<90°)得到另一条数轴y,x轴和y轴构成一个平面斜坐标系.规定:已知点P是平面斜坐标系中任意一点,过点P作y轴的平行线交x轴于点A,过点P作x轴的平行线交y轴于点B,若点A在x轴上对应的实数为a,点B在y轴上对应的实数为b,则称有序实数对(a,b)为点P的斜坐标.在平面斜坐标系中,若θ=45°,点P的斜坐标为(1,2![]() ),点G的斜坐标为(7,﹣2
),点G的斜坐标为(7,﹣2![]() ),连接PG,则线段PG的长度是_____.
),连接PG,则线段PG的长度是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为选拔一名选手参加“美丽邵阳,我为家乡做代言”主题演讲比赛,经研究,按图所示的项目和权数对选拔赛参赛选手进行考评(因排版原因统计图不完整).下表是李明、张华在选拔赛中的得分情况:
项目 选手 | 服装 | 普通话 | 主题 | 演讲技巧 |
李明 | 85 | 70 | 80 | 85 |
张华 | 90 | 75 | 75 | 80 |
结合以上信息,回答下列问题:
(1)求服装项目的权数及普通话项目对应扇形的圆心角大小;
(2)求李明在选拔赛中四个项目所得分数的众数和中位数;
(3)根据你所学的知识,帮助学校在李明、张华两人中选择一人参加“美丽邵阳,我为家乡做代言”主题演讲比赛,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,AB=AC,BD⊥AC,垂足为E,点F在BD的延长线上,且DF=DC,连接AF、CF.
(1)求证:∠BAC=2∠DAC;
(2)若AF=10,BC=4![]() ,求tan∠BAD的值.
,求tan∠BAD的值.
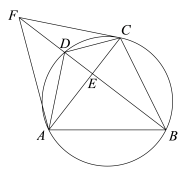
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代第一部自成体系的数学专著,代表了东方数学的最高成就.它的算法体系至今仍在推动着计算机的发展和应用.书中记载:“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”译为:“今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这木材,锯口深1寸(ED=1寸),锯道长1尺(AB=1尺=10寸)”,问这块圆形木材的直径是多少?”
如图所示,请根据所学知识计算:圆形木材的直径AC是( )
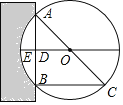
A. 13寸 B. 20寸 C. 26寸 D. 28寸
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com