
【题目】某校为选拔一名选手参加“美丽邵阳,我为家乡做代言”主题演讲比赛,经研究,按图所示的项目和权数对选拔赛参赛选手进行考评(因排版原因统计图不完整).下表是李明、张华在选拔赛中的得分情况:
项目 选手 | 服装 | 普通话 | 主题 | 演讲技巧 |
李明 | 85 | 70 | 80 | 85 |
张华 | 90 | 75 | 75 | 80 |
结合以上信息,回答下列问题:
(1)求服装项目的权数及普通话项目对应扇形的圆心角大小;
(2)求李明在选拔赛中四个项目所得分数的众数和中位数;
(3)根据你所学的知识,帮助学校在李明、张华两人中选择一人参加“美丽邵阳,我为家乡做代言”主题演讲比赛,并说明理由.

【答案】(1)服装项目的权数是10%,普通话项目对应扇形的圆心角是72°;(2)众数是85,中位数是82.5;(3)选择李明参加“美丽邵阳,我为家乡做代言”主题演讲比赛,理由见解析.
【解析】(1)根据扇形图用1减去其它项目的权重可求得服装项目的权重,用360度乘以普通话项目的权重即可求得普通话项目对应扇形的圆心角大小;
(2)根据统计表中的数据可以求得李明在选拔赛中四个项目所得分数的众数和中位数;
(3)根据统计图和统计表中的数据可以分别计算出李明和张华的成绩,然后比较大小,即可解答本题.
(1)服装项目的权数是:1﹣20%﹣30%﹣40%=10%,
普通话项目对应扇形的圆心角是:360°×20%=72°;
(2)明在选拔赛中四个项目所得分数的众数是85,中位数是:(80+85)÷2=82.5;
(3)李明得分为:85×10%+70×20%+80×30%+85×40%=80.5,
张华得分为:90×10%+75×20%+75×30%+80×40%=78.5,
∵80.5>78.5,
∴李明的演讲成绩好,
故选择李明参加“美丽邵阳,我为家乡做代言”主题演讲比赛.


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,点I是△ABC的内心,∠AIC=124°,点E在AD的延长线上,则∠CDE的度数为( )

A. 56° B. 62° C. 68° D. 78°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别用火柴棍连续搭建正三角形和正六边形,公共边只用一根火柴棍.如果搭建正三角形和正六边形共用了2018根火柴棍,并且正三角形的个数比正六边形的个数多7个,那么能连续搭建正三角形的个数是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,B、A、F三点在同一直线上,(1)AD∥BC,(2)∠B=∠C,(3)AD平分∠EAC.
请你用其中两个作为条件,另一个作为结论,构造一个真命题,并证明.
己知:______________________________________________________.
求证:______________________________________________________.
证明:

查看答案和解析>>
科目:初中数学 来源: 题型:
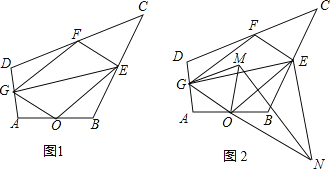
【题目】如图1所示,在四边形ABCD中,点O,E,F,G分别是AB,BC,CD,AD的中点,连接OE,EF,FG,GO,GE.
(1)证明:四边形OEFG是平行四边形;
(2)将△OGE绕点O顺时针旋转得到△OMN,如图2所示,连接GM,EN.
①若OE=![]() ,OG=1,求
,OG=1,求![]() 的值;
的值;
②试在四边形ABCD中添加一个条件,使GM,EN的长在旋转过程中始终相等.(不要求证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半径为1的![]() 的圆心A在抛物线y=(x-3)2-1上,AB//x轴交
的圆心A在抛物线y=(x-3)2-1上,AB//x轴交 ![]() 于点B(点B在点A的右侧),当点A在抛物线上运动时,点B随之运动得到的图象的函数表达式为( )
于点B(点B在点A的右侧),当点A在抛物线上运动时,点B随之运动得到的图象的函数表达式为( )

A. y=(x-4)2-1 B. y=(x-3)2 C. y=(x-2)2-1 D. y=(x-3)2-2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E在边AD上,将此矩形沿CE折叠,点D落在点F处,连接BF,B、F、E三点恰好在一直线上.
(1)求证:△BEC为等腰三角形;(2)若AB=2,∠ABE=45°,求矩形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市设计的长方形休闲广场如图所示,两端是两个半圆形的花坛,中间是一个直径为长方形宽度一半的圆形喷水池.
(1)用图中所标字母表示广场空地(图中阴影部分)的面积.
(2)若休闲广场的长为90米,宽为40米,求广场空地的面积(计算结果保留π).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com