
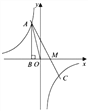
【题目】如图,已知反比例函数![]() 的图象经过第二象限内的点A(
的图象经过第二象限内的点A(![]() ,4),AB⊥x轴于点B,△AOB的面积为2,若直线
,4),AB⊥x轴于点B,△AOB的面积为2,若直线![]() 经过点A,并且经过反比例函数
经过点A,并且经过反比例函数![]() 的图象上另一点C(2,
的图象上另一点C(2,![]() ).
).
(1)求反比例函数和直线的解析式;
(2)设直线![]() 与
与![]() 轴交于点M,求AM的长.
轴交于点M,求AM的长.
【答案】(1) ![]() ,y=﹣2x+2;(2)2
,y=﹣2x+2;(2)2![]()
【解析】分析:
(1)由题意易得S△AOB=![]() AB·
AB·![]() ,这样结合已知条件即可求得m的值,从而可得点A的坐标,由点A的坐标求得k的值,即可得到反比例函数的解析式,再将点C的坐标代入所得的解析式求得n的值,可得点C的坐标,这样由直线
,这样结合已知条件即可求得m的值,从而可得点A的坐标,由点A的坐标求得k的值,即可得到反比例函数的解析式,再将点C的坐标代入所得的解析式求得n的值,可得点C的坐标,这样由直线![]() 过点A、C即可求得一次函数的解析式了;
过点A、C即可求得一次函数的解析式了;
(2)由(1)中所得一次函数的解析式求得点M的坐标,由此可得BM的长,这样结合AB的长即可由勾股定理求得AM的长了.
(1)∵点A(m,4)在第二象限,即AB=4,OB=|m|,
∵S△AOB=![]() AB·OB=
AB·OB=![]() AB·
AB·![]() ,
,
解得: |m|=1,
∴A (-1,4)
∵点A(-1,4)在反比例函数![]() 的图像上
的图像上
∴k=-4,
∴反比例函数解析式为![]() ,
,
又∵反比例函数![]() 的图象经过C(2,n)
的图象经过C(2,n)
∴n=-2,
∴C (2,﹣2),
∵直线y=ax+b过点A (﹣1,4),C (2,﹣2)
∴ ![]() ,
,
解方程组得:![]() ,
,
∴直线y=ax+b的解析式为y=﹣2x+2;
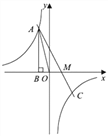
(2)当y=0时,即﹣2x+2=0,
解得x=1,
∴点M的坐标是M(1,0),
在Rt△ABM中,∵AB=4,BM=BO+OM=1+1=2,
∴AM=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,点O是直线AB上一点,∠AOC=40°,OD平分∠AOC,∠COE=70°.
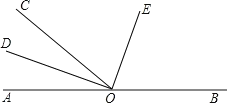
(1)请你说明DO⊥OE;
(2)OE平分∠BOC吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
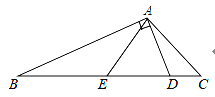
【题目】如图,在△ABC中,∠C=2∠B,点D为BC上一点,且AD⊥AB,点E是BD的中点,连接AE,且AE=DE.
(1)求证:∠AEC=∠C;
(2)若AE=8.5,AD=8,求△ABE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用方程解答下列问题
(1)一件工作,甲单独做20小时完成,乙单独做12小时完成,现在先由甲单独做4小时,余下的由甲乙一起完成余下的部分需要几小时完成?
(2)王强参加了一场3000米的赛跑,他以6米/秒的速度跑了一段路程,又以4米/秒的速度跑完了其余的路程,一共花了10分钟,王强以6米秒的速度跑了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图各图是棱长为1cm的小正方体摆成的,如图①中,从正面看有1个正方形,表面积为6cm2;如图②中,从正面看有3个正方形,表面积为18cm2;如图③,从正面看有6个正方形,表面积为36cm2;…
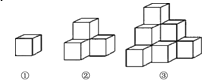
(1)第6个图中,从正面看有多少个正方形?表面积是多少?
(2)第n个图形中,从正面看有多少个正方形?表面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点C是直线AB上一点,AC=6cm,BC=4cm,点M、N分别是AC、BC的中点;
(1)如图,点C在线段AB上,求线段MN的长;
(2)若点C在线段AB的延长线上,其他条件不变,则线段MN的长为_______cm.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com