
【题目】根据题意解答
(1)【阅读发现】如图①,在正方形ABCD的外侧,作两个等边三角形ABE和ADF,连结ED与FC交于点M,则图中△ADE≌△DFC,可知ED=FC,求得∠DMC= .
(2)【拓展应用】如图②,在矩形ABCD(AB>BC)的外侧,作两个等边三角形ABE和ADF,连结ED与FC交于点M. 
(i)求证:ED=FC.
(ii)若∠ADE=20°,求∠DMC的度数.
【答案】
(1)90°
(2)(i)证明:∵△ABE为等边三角形,
∴∠EAB=60°,EA=AB.
∵△ADF为等边三角形,
∴∠FDA=60°,AD=FD.
∵四边形ABCD为矩形,
∴∠BAD=∠ADC=90°,DC=AB.
∴EA=DC.
∵∠EAD=∠EAB+∠BAD=150°,∠CDF=∠FDA+∠ADC=150°,
∴∠EAD=∠CDF.
在△EAD和△CDF中,
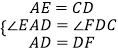 ,
,
∴△EAD≌△CDF.
∴ED=FC
(ii)∵△EAD≌△CDF,
∴∠ADE=∠DFC=20°,
∴∠DMC=∠FDM+∠DFC=∠FDA+∠ADE+∠DFC=60°+20°+20°=100°
【解析】解:如图①中,∵四边形ABCD是正方形, ∴AD=AB=CD,∠ADC=90°,
∵△ADE≌△DFC,
∴DF=CD=AE=AD,
∵∠FDC=60°+90°=150°,
∴∠DFC=∠DCF=∠ADE=∠AED=15°,
∴∠FDE=60°+15°=75°,
∴∠MFD+∠FDM=90°,
∴∠FMD=90°,
所以答案是90°
【考点精析】关于本题考查的矩形的性质和正方形的性质,需要了解矩形的四个角都是直角,矩形的对角线相等;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】计算
(1)﹣18×(﹣2)÷3
(2)(﹣![]() )×(﹣90)÷
)×(﹣90)÷![]()
(3)﹣2.5÷![]() ×(﹣
×(﹣![]() );
);
(4)(﹣10)2﹣[16+(﹣3)2]
(5)(![]() ﹣
﹣![]() +2)÷
+2)÷![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2﹣2x与x轴正半轴相交于点A,顶点为B.
(1)用含a的式子表示点B的坐标;
(2)经过点C(0,﹣2)的直线AC与OB(O为原点)相交于点D,与抛物线的对称轴相交于点E,△OCD≌△BED,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=﹣x2+2x+3与x轴的交点为A,B(点A在点B的左侧),与y轴的交点为C,连结BC.点M是抛物线上A,C之间的一个动点,过点M作MN∥BC,分别交x轴、抛物线于D,N,过点M作EF⊥x轴,垂足为F,并交直线BC于点E,
(1)求点A,B,C的坐标.
(2)当点M恰好是EF的中点,求BD的长.
(3)连接DE,记△DEM,△BDE的面积分别为S1 , S2 , 当BD=1时,则S2﹣S1= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】东东想把一根70 cm长的木棒放到一个长、宽、高分别为30 cm,40 cm,50 cm的木箱中,他能放进去吗?答:______. (填“能”或“不能”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O中,点A为 ![]() 中点,BD为直径,过A作AP∥BC交DB的延长线于点P.
中点,BD为直径,过A作AP∥BC交DB的延长线于点P. 
(1)求证:PA是⊙O的切线;
(2)若 ![]() ,AB=6,求sin∠ABD的值.
,AB=6,求sin∠ABD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为⊙O上的一点,P为直径AB延长线上的一点,BH⊥CP于H交⊙O于D,∠PBH=2∠PAC. 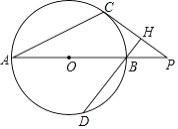
(1)求证:PC是⊙O的切线;
(2)若sin∠P= ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某面粉加工厂加工的面粉,用每袋可装10g面粉的袋子装了200袋经过称重,质量超过标准质量10kg的用正数表示,质量低于标准质量10kg的用负数表示,结果记录如下
与标准质量的偏差(kg) | ﹣1.5 | ﹣1 | ﹣0.5 | 0 | 0.5 | 1 | 2 |
袋数(袋) | 40 | 30 | 10 | 25 | 40 | 20 | 35 |
(1)求这批面粉的总质量;
(2)如果100kg小麦加工80kg面粉,那么这批面粉是由多少千克小麦加工的?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com