
【题目】
(1) 填空:AB=_________,BC= ;
(2) 若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒3个单位长度和7个单位长度的速度向右运动.设运动时间为t秒,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB,用含t的代数式表示BC和AB的长,并探索:BC-AB的值是否随着时间t的变化而改变?请说明理由
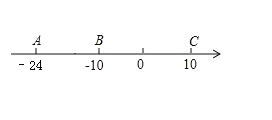
【答案】(1)、AB=14;BC=20;(2)、不变
【解析】试题分析:(1)、根据两点之间的距离公式求出AB和BC的长度;(2)、首先分别用含t的代数式表示A、B、C三点所表示的数,然后分别求出BC和AB的长度,然后进行计算.
试题解析:(1)、AB=﹣10﹣(﹣24)=14,BC=10﹣(﹣10)=20.
(2)、不变. ∵经过t秒后,A、B、C三点所对应的数分别是﹣24﹣t,﹣10+3t,10+7t,
∴BC=(10+7t)﹣(﹣10+3t)=4t+20, AB=(﹣10+3t)﹣(﹣24﹣t)=4t+14,
∴BC﹣AB=(4t+20)﹣(4t+14)=6. ∴BC﹣AB的值不会随着时间t的变化而改变.


科目:初中数学 来源: 题型:
【题目】在一次射击练习中,某运动员命中的环数是7,9,9,10,10,其中9是( )
A. 平均数 B. 中位数 C. 众数 D. 既是平均数和中位数,又是众数
查看答案和解析>>
科目:初中数学 来源: 题型:
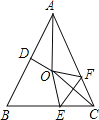
【题目】如图,在等腰△ABC中,AB=AC,∠BAC=50°,∠BAC的角平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠CEF的度数是______________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC的三个内角∠A、∠B、∠C满足关系式∠B+∠C=∠A,则此三角形( )
A. 一定有一个内角为45° B. 一定有一个内角为60°
C. 一定是直角三角形 D. 一定是钝角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB为⊙O的直径,点C、D在⊙O上,且BC=6cm,AC=8cm,∠ABD=45°.
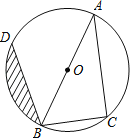
(1)求BD的长;
(2)求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,阅读下面的题目及分析过程,并按要求进行证明.
已知:如图,E是BC的中点,点A在DE上,且∠BAE=∠CDE. 求证:AB=CD.
分析:证明两条线段相等,常用的一般方法是应用全等三角形或等腰三角形的判定和性质,观察本题中要要证AB=CD,必须添加适当的辅助线,构造全等三角形或等腰三角形请用二种不同的方法证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com