考点:抛物线与x轴的交点,二次函数图象上点的坐标特征
专题:
分析:(1)当x=0时可求得点C坐标,当y=0时可求得点A,B坐标,即可解题;
(2)根据A,B坐标可以求得AB长度,根据C点坐标可以求得OC长度,即可解题;
(3)存在,根据S
△ABP=S
△ABC可得点P纵坐标与点C纵坐标相等,且为3,即可求得点P坐标;
(4)存在,根据S
△ABP=
S
△ABC可得点P纵坐标为4,即可求得点P坐标;
(5)不存在,根据S
△ABP=
S
△ABC可得点P纵坐标为5,方程无解,故不存在.
解答:解:(1)当x=0时,y=0+0+3=3,
∴C点坐标为(0,3),
当y=0时,0=-x
2+2x+3,整理得:x
2-2x-3=0,
解得:x=-1或3,
∵A点在B点左侧,
∴A(-1,0),B(3,0);
(2)∴S
△ABC=
AB•OC=6;
(3)存在,
∵S
△ABP=S
△ABC,
∴点P纵坐标与点C纵坐标相等,且为3,
∴-x
2+2x+3=3,
解得:x=2或0,∴点P坐标为(2,3);
(4)存在,
∵S
△ABP=
S
△ABC,
∴点P纵坐标为点C纵坐标
倍,即为4,
∴-x
2+2x+3=4,
解得:x=1,∴点P坐标为(1,4);
(5)不存在,
∵S
△ABP=
S
△ABC,
∴点P纵坐标为点C纵坐标
倍,即为5,
∴-x
2+2x+3=5,
解得:x无解,∴不存在点P.
点评:本题考查了抛物线和坐标轴交点的求解,考查了抛物线上点的求解,本题中求得△ABC的面积是解题的关键.

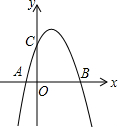 已知抛物线的表达式为y=-x2+2x+3.
已知抛物线的表达式为y=-x2+2x+3.

 如图,⊙O是直径BC,弦AB,∠BAC的平分线交⊙O于点D.
如图,⊙O是直径BC,弦AB,∠BAC的平分线交⊙O于点D.