
ЁОЬтФПЁПвбжЊAЃЌBЃЌCЃЌDЃЌEЃЌFЗжБ№ЪЧЁбOЩЯЕФСљЕШЗжЕуЃЌЁбOЕФАыОЖЪЧ100ЃЌдкетСљЕуМфаоНЈЛЅЭЈЕФЕРТЗЃЈМДЭМжаЪЕЯпВПЗжЮЊЕРТЗЃЉЃЌЯжгаШчЯТСНжжЗНАИЃЎЗНАИвЛЃКШчЭМ1ЃЌИїЬѕЯпЖЮГЄЖШОљЯрЕШЃЌМЧЭМжаЕРТЗГЄЮЊl1ЃЛЗНАИЖўЃКШчЭМ2ЃЌAQ=BG=CH=DM=EN=FPЃЌЕуGЃЌHЃЌMЃЌNЃЌPЃЌQЗжБ№ЪЧЯпЖЮAQЃЌBGЃЌCHЃЌDMЃЌENЃЌFPЕФжаЕуЃЌСљБпаЮGHMNPQЪЧвдOЮЊжааФЕФе§СљБпаЮЃЌМЧЭМжаЕРТЗГЄЮЊl2ЃЛдђl1= ЃЛl2= ЃЎ 
ЁОД№АИЁП![]() ЃЛ
ЃЛ![]()
ЁОНтЮіЁПНтЃКШчЭМ1ЃЌСЌНгOAЃЌOBЃЌЙ§ЕуMзїMG![]() OAгкЕуGЃЌ
OAгкЕуGЃЌ
ЁпAЃЌBЃЌCЃЌDЃЌEЃЌFЗжБ№ЪЧЁбOЩЯЕФСљЕШЗжЕуЃЌЁбOЕФАыОЖЪЧ100ЃЌ
Ёр![]() AOB=60
AOB=60![]() ЃЌ
ЃЌ
ЁпИїЬѕЯпЖЮГЄЖШОљЯрЕШЃЌ
Ёр![]() AOM=30
AOM=30![]() ЃЌ
ЃЌ
дкRt![]() OMGжаЃЌЁпOG=
OMGжаЃЌЁпOG=![]() OA=50ЃЌЁрOM=
OA=50ЃЌЁрOM=![]() ЃЌ
ЃЌ
Ёрl1=![]()
![]() 9=
9=![]() .
.
ШчЭМ2ЃЌСЌНгOBЃЌЙ§ЕуOзїORЁЭBFгкЕуRЃЌ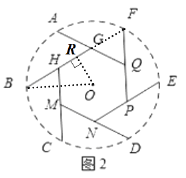
ЁпAQ=BG=CH=DM=EN=FPЃЌЕуGЃЌHЃЌMЃЌNЃЌPЃЌQЗжБ№ЪЧЯпЖЮAQЃЌBGЃЌCHЃЌDMЃЌENЃЌFPЕФжаЕуЃЌСљБпаЮGHMNPQЪЧвдOЮЊжааФЕФе§СљБпаЮЃЌЁрбгГЄBGФмгыЕуFжиКЯЃЌЕуHКЭЕуGЪЧBFЕФШ§ЕШЗжЕу.
дкRt Ёї OBRжаЃЌЁп![]() OBR=30 Ёу ЃЌOB=100ЃЌЁрBR=
OBR=30 Ёу ЃЌOB=100ЃЌЁрBR=![]() ЃЌЁрBF=
ЃЌЁрBF=![]() ЃЌ
ЃЌ
ЁрBG=![]() BF=
BF=![]() ЃЌ
ЃЌ
Ёрl2=![]()
![]() 6=
6=![]() .
.
ЫљвдД№АИЪЧЃК![]() ЃЛ
ЃЛ![]() .
.
ЁОПМЕуОЋЮіЁПРћгУе§ЖрБпаЮЕФаджЪКЭе§ЖрБпаЮКЭдВЖдЬтФПНјааХаЖЯМДПЩЕУЕНД№АИЃЌашвЊЪьжЊе§ЖрБпаЮЖМЪЧжсЖдГЦЭМаЮЃЎвЛИіе§nБпаЮЙВгаnЬѕЖдГЦжсЃЌУПЬѕЖдГЦжсЖМЭЈЙ§е§nБпаЮЕФжааФ;е§ЖрБпаЮЕФжааФБпЪ§ЮЊХМЪ§ЕФе§ЖрБпаЮЪЧжааФЖдГЦЭМаЮЃЌЫќЕФЖдГЦжааФЪЧе§ЖрБпаЮЕФжааФЃЛдВЕФФкНгЫФБпаЮЕФЖдНЧЛЅВЙЃЌВЂЧвШЮКЮвЛИіЭтНЧЖМЕШгкЫќЕФФкЖдНЧЃЛдВЕФЭтЧаЫФБпаЮЕФСНзщЖдБпЕФКЭЯрЕШЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊдкRtЁїABCжаЃЌЁЯACB=90ЁуЃЌЯжАДШчЯТВНжшзїЭМЃК
ЂйЗжБ№вдAЃЌCЮЊдВаФЃЌaЮЊАыОЖЃЈaЃО ![]() ACЃЉзїЛЁЃЌСНЛЁЗжБ№НЛгкMЃЌNСНЕуЃЛ
ACЃЉзїЛЁЃЌСНЛЁЗжБ№НЛгкMЃЌNСНЕуЃЛ
ЂкЙ§MЃЌNСНЕузїжБЯпMNНЛABгкЕуDЃЌНЛACгкЕуEЃЛ
ЂлНЋЁїADEШЦЕуEЫГЪБеыа§зЊ180ЁуЃЌЩшЕуDЕФЯёЮЊЕуFЃЎ
ЃЈ1ЃЉЧыдкЭМжажБЯпБъГіЕуFВЂСЌНгCFЃЛ
ЃЈ2ЃЉЧѓжЄЃКЫФБпаЮBCFDЪЧЦНааЫФБпаЮЃЛ
ЃЈ3ЃЉЕБЁЯBЮЊЖрЩйЖШЪБЃЌЫФБпаЮBCFDЪЧСтаЮЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌODЁЭЯвBCгкЕуFЃЌНЛЁбOгкЕуEЃЌСЌНсCEЁЂAEЁЂCDЃЌШєЁЯAEC=ЁЯODCЃЎ 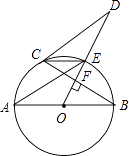
ЃЈ1ЃЉЧѓжЄЃКжБЯпCDЮЊЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉШєAB=5ЃЌBC=4ЃЌЧѓЯпЖЮCDЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєЙигкxЕФвЛдЊЖўДЮЗНГЬЉx2+2ax+2Љ3a=0ЕФвЛИљx1Ён1ЃЌСэвЛИљx2ЁмЉ1ЃЌдђХзЮяЯпy=Љx2+2ax+2Љ3aЕФЖЅЕуЕНxжсОрРыЕФзюаЁжЕЪЧ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЃЌЖдгкPЃЈaЃЌbЃЉКЭЕуQЃЈaЃЌbЁфЃЉЃЌИјГіШчЯТЖЈвхЃКШєbЁф= ![]() ЃЌдђГЦЕуQЮЊЕуPЕФЯоБфЕуЃЎР§ШчЃКЕуЃЈ2ЃЌ3ЃЉЕФЯоБфЕуЕФзјБъЪЧЃЈ2ЃЌ3ЃЉЃЌЕуЃЈЉ2ЃЌ5ЃЉЕФЯоБфЕуЕФзјБъЪЧЃЈЉ2ЃЌЉ5ЃЉЃЎ
ЃЌдђГЦЕуQЮЊЕуPЕФЯоБфЕуЃЎР§ШчЃКЕуЃЈ2ЃЌ3ЃЉЕФЯоБфЕуЕФзјБъЪЧЃЈ2ЃЌ3ЃЉЃЌЕуЃЈЉ2ЃЌ5ЃЉЕФЯоБфЕуЕФзјБъЪЧЃЈЉ2ЃЌЉ5ЃЉЃЎ
ЃЈ1ЃЉЕуЃЈ ![]() ЃЌ1ЃЉЕФЯоБфЕуЕФзјБъЪЧЃЛ
ЃЌ1ЃЉЕФЯоБфЕуЕФзјБъЪЧЃЛ
ЃЈ2ЃЉХаЖЯЕуAЃЈЉ2ЃЌЉ1ЃЉЁЂBЃЈЉ1ЃЌ2ЃЉжаЃЌФФвЛИіЕуЪЧКЏЪ§y= ![]() ЭМЯѓЩЯФГвЛИіЕуЕФЯоБфЕуЃПВЂЫЕУїРэгЩЃЛ
ЭМЯѓЩЯФГвЛИіЕуЕФЯоБфЕуЃПВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШєЕуPЃЈaЃЌbЃЉдкКЏЪ§y=Љx+3ЕФЭМЯѓЩЯЃЌЦфЯоБфЕуQЃЈaЃЌbЁфЃЉЕФзнзјБъЕФШЁжЕЗЖЮЇЪЧЉ6ЁмbЁфЁмЉ3ЃЌЧѓaЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌОиаЮABCDЕФБпAB=4ЃЌЧвBCЃОABЃЌвЛИіСПНЧЦїШчЭМЫљЪОЗХжУЃЌЦфжаСуПЬЖШЃЈМДАыдВOЕФжБОЖЃЉгыБпABжиКЯЃЌЕуAДІЪЧ0ПЬЖШЃЌЕуBДІЪЧ180ПЬЖШЃЌЕуPЪЧСПНЧЦїЕФАыдВЛЁЩЯвЛЖЏЕуЃЌЙ§ЕуPзїАыдВЕФЧаЯпЃЌЩшЕуPЕФПЬЖШЪ§ЮЊmЃЌЙ§ЕуPЕФЧаЯпНЛЯпЖЮBCгыЯпЖЮADгкЕуEЃЌFЃЎ
ЃЈ1ЃЉЩшЁЯPAB=nЃЎ
ЂйШчЭМ1ЃЌЕБm=114ЁуЪБЃЌn=ЃЛ
ЂкжБНгаДГіnгыmЕФЙиЯЕЪНЃКЃЛ
ЃЈ2ЃЉЪдЫЕУїAFЁЄBEЪЧЗёЪЧвЛИіЖЈжЕЃЌШєЪЧЃЌЧыЧѓГіЫќЕФжЕЃЛШєВЛЪЧЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЕБEF= ![]() ЪБЃЌЧѓЕуPЕФПЬЖШЪ§mЕФжЕЃЎ
ЪБЃЌЧѓЕуPЕФПЬЖШЪ§mЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМзЁЂввСНЙЋЫОЮЊЁАМћвхгТЮЊЛљН№ЛсЁБИїОшПю60000дЊЃЌвбжЊввЙЋЫОБШМзЙЋЫОШЫОљЖрОш40дЊЃЌМзЙЋЫОЕФШЫЪ§БШввЙЋЫОЕФШЫЪ§Жр20%ЃЎ
ЧыФуИљОнвдЩЯаХЯЂЃЌЬсГівЛИігУЗжЪНЗНГЬНтОіЕФЮЪЬтЃЌВЂаДГіНтД№Й§ГЬЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЪ§бЇаЁзщгУИпЮЊ1.2УзЕФвЧЦїВтСПвЛНЬбЇТЅЕФИпCDЃЌШчЭМЃЌОрCDвЛЖЈОрРыЕФAДІЃЌгУвЧЦїВтЕУНЬбЇТЅЖЅВПDЕФбіНЧЮЊІТЃЌдйдкAгыCжЎМфбЁвЛЕуBЃЌгЩBДІВтГіНЬбЇТЅЖЅВПDЕФбіНЧЮЊІСЃЌВтЕУAЃЌBжЎМфЕФОрРыЮЊ4УзЃЌШєtanІС=1.6ЃЌtanІТ=1.2ЃЌдђЫћУЧФмЧѓГіНЬбЇТЅЕФИпТ№ЃП 
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃЯыСЫНтбЇЩњУПжмЕФПЮЭтдФЖСЪБМфЧщПіЃЌЫцЛњЕїВщСЫВПЗжбЇЩњЃЌЖдбЇЩњУПжмЕФПЮЭтдФЖСЪБМфxЃЈЕЅЮЛЃКаЁЪБЃЉНјааЗжзщећРэЃЌВЂЛцжЦСЫШчЭМЫљЪОЕФВЛЭъећЕФЦЕЪ§ЗжВМжБЗНЭМКЭЩШаЮЭГМЦЭМЃЎ ИљОнЭМжаЬсЙЉЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉВЙШЋЦЕЪ§ЗжВМжБЗНЭМЃЛ
ЃЈ2ЃЉЧѓЩШаЮЭГМЦЭМжаmЕФжЕКЭЁАEЁБзщЖдгІЕФдВаФНЧЖШЪ§ЃЛ
ЃЈ3ЃЉЧыЙРМЦИУаЃ3000УћбЇЩњжаУПжмЕФПЮЭтдФЖСЪБМфВЛаЁгк6аЁЪБЕФШЫЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com