练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，将△ABC沿射线BC方向平移得到△DEF，边DE与AC相交于点G，如果BC=3cm，△ABC的面积为9cm2，△EGC的面积等于4cm2，那么BE=　 　cm．

    　


    1考点： 相似三角形的判定与性质；平移的性质． 

    分析： 易证△ABC∽△GEC，根据相似三角形的面积的比等于相似比的平方，即可求得EC的长，则BE即可求解．

    解答： 解：∵AB∥DE，

    ∴△ABC∽△GEC，

    ∴=（）2=，

    ∴EC=2cm，

    ∴BE=BC﹣EC=3﹣2=1cm．

    故答案是：1

    点评： 本题考查了平移的性质，以及相似三角形的性质，正确理解性质求得EC的长是关键．

    　

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图所示，等腰三角形ABC的底边长为8cm，腰长为5cm，一动点P在底边上从B向C以0.25m/s的速度运动，当点P运动到PA与腰垂直的位置时，求点P运动的时间．

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    一个三角形的两边长分别为4cm和7cm，第三边长是一元二次方程x2﹣10x+21=0的实数根，则三角形的周长是cm．

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


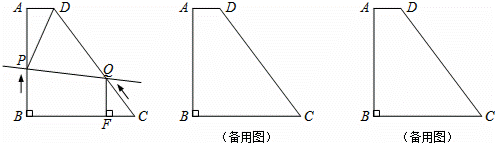
    如图，已知直角梯形ABCD中，AD∥BC，AB⊥BC，AD=2，AB=8，CD=10．

    （1）求梯形ABCD的面积；

    （2）动点P从点B出发，以2个单位/s的速度沿B→A→D→C方向向点C运动；动点Q从点C出发，以2个单位/s的速度沿C→D→A方向向点A运动；过点Q作QF⊥BC于点F．若P、Q两点同时出发，当其中一点到达终点时另一点也随之停止运动，设运动时间为t秒．问：

    ①当点P在B→A上运动时，是否存在这样的t，使得直线PQ将梯形ABCD的周长平分？若存在，请求出t的值，并判断此时PQ是否平分梯形ABCD的面积；若不存在，请说明理由．

    ②在运动过程中，是否存在这样的t，使得以P、D、Q为顶点的三角形恰好是以DQ为一腰的等腰三角形？若存在，请求出所有符合条件的t的值；若不存在，请说明理由．

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，△ABC与△DEA是两个全等的等腰直角三角形，∠BAC=∠D=90°，BC分别与AD、AE相交于点F、G．图中共有n对三角形相似（相似比不等于1），则n的值是（　　）

    　 A． 2 B． 3 C． 4 D． 5

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    解下列方程：2x2﹣4x﹣1=0．

     　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某批发商以40元/千克的成本价购入了某产品700千克，据市场预测，该产品的销售价y（元/千克）与保存时间x（天）的函数关系为y=50+2x，但保存这批产品平均每天将损耗15千克，且最多保存15天．另外，批发商每天保存该批产品的费用为50元．

    （1）若批发商在保存该产品5天时一次性卖出，则可获利　9250　元．

    （2）如果批发商希望通过这批产品卖出获利10000元，则批发商应在保存该产品多少天时一次性卖出？

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


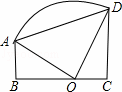
    如图，在梯形ABCD中，AB∥DC，AB⊥BC，AB=2cm，CD=4cm．以BC上一点O为圆心的圆经过A、D两点，且∠AOD=90°，则圆心O到弦AD的距离是cm．

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知：▱ABCD的两边AB，AD的长是关于x的方程x2﹣mx+﹣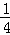=0的两个实数根．

    （1）当m为何值时，四边形ABCD是菱形？求出这时菱形的边长；

    （2）若AB的长为2，那么▱ABCD的周长是多少？

    　

    查看答案和解析>>

    同步练习册答案