
如图,已知直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,AB=8,CD=10.
(1)求梯形ABCD的面积;
(2)动点P从点B出发,以2个单位/s的速度沿B→A→D→C方向向点C运动;动点Q从点C出发,以2个单位/s的速度沿C→D→A方向向点A运动;过点Q作QF⊥BC于点F.若P、Q两点同时出发,当其中一点到达终点时另一点也随之停 止运动,设运动时间为t秒.问:
止运动,设运动时间为t秒.问:
①当点P在B→A上运动时,是否存在这样的t,使得直线PQ将梯形ABCD的周长平分?若存在,请求出t的值,并判断此时PQ是否平分梯形ABCD的面积;若不存在,请说明理由.
②在运动过程中,是否存在这样的t,使得以P、D、Q为顶点的三角形恰好是以DQ为一腰的等腰三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.
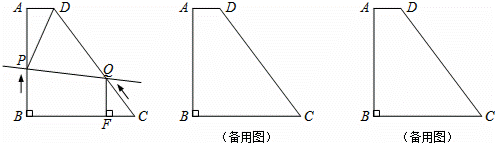
解:(1)如图(1)过D作DH∥AB交BC于点H,
∵AD∥BC,DH∥AB,
∴四边形ABHD是平行四边形,
∴DH=AB=8,BH=AD=2,
∵CD=10,
∴HC= =6,
=6,
∴BC=BH+CH=8,
∴SABCD= (AD+BC)•AB=
(AD+BC)•AB= ×(2+8)×8=40;
×(2+8)×8=40;
(2)①∵BP=CQ=2t,
∴AP=8﹣2t,DQ=10﹣2t,
∵AP+AD+DQ=PB+BC+CQ,
∴8﹣2t+2+10﹣2t=2t+8+2t,
∴t= <4,
<4,
∴当t= 秒时,PQ将梯形ABCD周长平分,
秒时,PQ将梯形ABCD周长平分,
QC=3,PB=3,
∵QE∥DH,
∴ =
= =
= ,
,
∴ =
= =
= ,
,
∴QE= ,EC=
,EC= ,
,
BE=8﹣ =
= ,
,
∴四边形PBCQ面积=S梯形AEBP+S△QEC=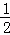 (PB+QE)×BE+
(PB+QE)×BE+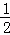 QE×EC=
QE×EC=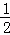 (
( +3)×
+3)× +
+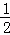 ×
× ×
× =
= =18.9,
=18.9,
∴PQ不平分梯形ABCD的面积;
②第一种情况:如图(2),当0≤t≤4时,过Q点作QE⊥BC,QH⊥AB,垂足为E,H,
∵AP=8﹣2t,AD=2,
∴PD= =
= ,
,
∵CE= t,QE=
t,QE= t,
t,
∴QH=BE=8﹣ t,BH=QE=
t,BH=QE= t,
t,
∴PH=2t﹣ t=
t= t,
t,
∴PQ= =
= =
= ,
,
DQ=10﹣2t,
I:DQ=DP,10﹣2t= ,
,
解得;t=4秒,
Ⅱ:DQ=PQ,10﹣2t= ,
,
化简得:3t2﹣26t+45=0,
解得;t= ,t=
,t= >4(不合题意,舍去),
>4(不合题意,舍去),
∴t= ,
,
第二种情况:当4≤t<5时,DP=DQ=10﹣2t,
∴当4≤t<5时,以DQ为腰的等腰△DPQ恒成立,
第三种情况:5<t≤6时,DP=DQ=2t﹣10,
∴5<t≤6时,以DQ为腰的等腰△DPQ恒成立,
综上所述,t= 或4,4≤t<5或,5<t≤6时以DQ为腰的等腰△DPQ恒成立.
或4,4≤t<5或,5<t≤6时以DQ为腰的等腰△DPQ恒成立.




科目:初中数学 来源: 题型:
雅安地震牵动着全国人民的心,某单位开展了“一方有难,八方支援”赈灾捐款活动.第一天收到捐款10 000元,第三天收到捐款12 100元.
(1)如果第二天、第三天收到捐款的增长率相同,求捐款增长率;
(2)按照(1)中收到捐款的增长率速度,第四天该单位能收到多少捐款?
查看答案和解析>>
科目:初中数学 来源: 题型:
在平面直角坐标系中,将函数y=2x2的图象先向右平移1个单位,再向上平移5个单位得到图象的函数关系式是( )
A. y=2(x﹣1)2﹣5 B. y=2(x﹣1)2+5 C. y=2(x+1)2﹣5 D. y=2(x+1)2+5
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,将△ABC沿射线BC方向平移得到△DEF,边DE与AC相交于点G,如果BC=3cm,△ABC的面积为9cm2,△EGC的面积等于4cm2,那么BE= cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
下列说法中,正确的是( )
A.同一条弦所对的两条弧一定是等弧
B.长度相等的两条弧是等弧
C.两条直线被一组平行线所截,所得的对应线段成比例
D.三角形的外心到三角形各边的距离相等
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com