
【题目】如图1,在Rt△ABC中,∠C=90°,AC=BC=2,点D、E分别在边AC、AB上,AD=DE=![]() AB,连接DE.将△ADE绕点A逆时针方向旋转,记旋转角为θ.
AB,连接DE.将△ADE绕点A逆时针方向旋转,记旋转角为θ.
(1)问题发现
①当θ=0°时,![]() = ;
= ;
②当θ=180°时,![]() = .
= .
(2)拓展探究
试判断:当0°≤θ<360°时,![]() 的大小有无变化?请仅就图2的情形给出证明;
的大小有无变化?请仅就图2的情形给出证明;
(3)问题解决
①在旋转过程中,BE的最大值为 ;
②当△ADE旋转至B、D、E三点共线时,线段CD的长为 .

【答案】(1)①![]() ;(2)详见解析;(3)①2
;(2)详见解析;(3)①2![]() +2
+2![]() +1或
+1或![]() ﹣1.
﹣1.
【解析】分析:(1)①先判断出DE∥CB,进而得出比例式,代值即可得出结论;
②先得出DE∥BC,即可得出,![]() ,再用比例的性质即可得出结论;
,再用比例的性质即可得出结论;
(2)先∠CAD=∠BAE,进而判断出△ADC∽△AEB即可得出结论;
(3)分点D在BE的延长线上和点D在BE上,先利用勾股定理求出BD,再借助(2)结论即可得出CD.
详解:(1)①当θ=0°时,
在Rt△ABC中,AC=BC=2,
∴∠A=∠B=45°,AB=2![]() ,
,
∵AD=DE=![]() AB=
AB=![]() ,
,
∴∠AED=∠A=45°,
∴∠ADE=90°,
∴DE∥CB,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
故答案为:![]() ,
,
②当θ=180°时,如图1,
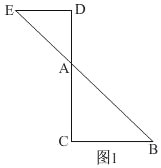
∵DE∥BC,
∴![]() ,
,
∴![]() ,
,
即:![]() ,
,
∴![]() ,
,
故答案为:![]() ;
;
(2)当0°≤θ<360°时,![]() 的大小没有变化,
的大小没有变化,
理由:∵∠CAB=∠DAE,
∴∠CAD=∠BAE,
∵![]() ,
,
∴△ADC∽△AEB,
∴![]() ;
;
(3)①当点E在BA的延长线时,BE最大,
在Rt△ADE中,AE=![]() AD=2,
AD=2,
∴BE最大=AB+AE=2![]() +2;
+2;
②如图2,
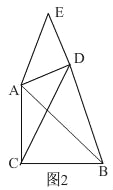
当点E在BD上时,
∵∠ADE=90°,
∴∠ADB=90°,
在Rt△ADB中,AB=2![]() ,AD=
,AD=![]() ,根据勾股定理得,BD=
,根据勾股定理得,BD=![]() =
=![]() ,
,
∴BE=BD+DE=![]() +
+![]() ,
,
由(2)知,![]() ,
,
∴CD=![]() +1,
+1,
如图3,
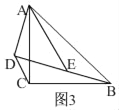
当点D在BE的延长线上时,
在Rt△ADB中,AD=![]() ,AB=2
,AB=2![]() ,根据勾股定理得,BD=
,根据勾股定理得,BD=![]() =
=![]() ,
,
∴BE=BD﹣DE=![]() ﹣
﹣![]() ,
,
由(2)知,![]() ,
,
∴CD=![]() ﹣1.
﹣1.
故答案为:![]() +1或
+1或![]() ﹣1.
﹣1.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
【题目】已知y﹣2与x成正比例,当x=2时,y=6.
(1)求y与x之间的函数解析式.
(2)在所给直角坐标系中画出函数图象.
(3)由函数图象直接写出当﹣2≤y≤2时,自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
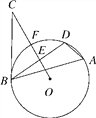
【题目】如图,△ABD是⊙O的内接三角形,E是弦BD的中点,点C是⊙O外一点,且∠DBC=∠A,连接OE并延长与⊙O相交于点F,与BC相交于点C.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为6,BC=8,求弦BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.
(1)求每台A型电脑和B型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
①求y关于x的函数关系式;
②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?
(3)实际进货时,厂家对A型电脑出厂价下调m(0<m<100)元,且限定商店最多购进A型电脑70台.若商店保持两种电脑的售价不变,请你根据以上信息及(2)中条件,设计出使这100台电脑销售总利润最大的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,AC=6,BC=8,点D、E分别是斜边AB和直角边BC上的点,把△ABC沿着直线DE折叠,顶点B的对应点是点B′.
(1)如图①,如果点B′和点A重合,求CE的长.
(2)如图②,如果点B′落在直角边AC的中点上,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,□ABCD中,对角线AC与AB、AD的夹角分别为α、β,点E是AC上任意一点,给出如下结论:①AB sinα=AD sinβ;②S△ABE=S△ADE;③ADsinα=AB sinβ. 其中正确的个数有( )
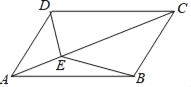
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
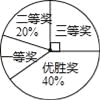
【题目】国务院办公厅在2015年3月16日发布了《中国足球发展改革总体方案》,这是中国足球史上的重大改革,为进一步普及足球知识,传播足球文化,我市某区在中小学举行了“足球在身边”知识竞赛,各类获奖学生人数的比例情况如图所示,其中获得三等奖的学生共50名,请结合图中信息,解答下列问题:
(1)获得一等奖的学生人数;
(2)在本次知识竞赛活动中,A,B,C,D四所学校表现突出,现决定从这四所学校中随机选取两所学校举行一场足球友谊赛,请用画树状图或列表的方法求恰好选到A,B两所学校的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A=3a2b-2ab2+abc,小明同学错将“2A-B”看成“2A+B”,算得结果为4a2b-3ab2+4abc.
(1)求出2A-B的结果;
(2)小强同学说(1)中的结果的大小与c的取值无关,正确吗?若a=![]() ,b=
,b=![]() ,求(1)中式子的值.
,求(1)中式子的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com