
【题目】如图,△ABD是⊙O的内接三角形,E是弦BD的中点,点C是⊙O外一点,且∠DBC=∠A,连接OE并延长与⊙O相交于点F,与BC相交于点C.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为6,BC=8,求弦BD的长.
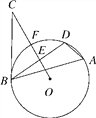
【答案】(1)证明见解析(2)9.6
【解析】试题分析:(1)连接OB,由垂径定理可得BE=DE,OE⊥BD,![]() ,再由圆周角定理可得
,再由圆周角定理可得![]() ,从而得到∠ OBE+∠ DBC=90°,即
,从而得到∠ OBE+∠ DBC=90°,即![]() ,命题得证.
,命题得证.
(2)由勾股定理求出OC,再由△OBC的面积求出BE,即可得出弦BD的长.
试题解析:(1)证明:如下图所示,连接OB.
∵ E是弦BD的中点,∴ BE=DE,OE⊥ BD,![]() ,
,
∴∠ BOE=∠ A,∠ OBE+∠ BOE=90°.
∵∠ DBC=∠ A,∴∠ BOE=∠ DBC,
∴∠ OBE+∠ DBC=90°,∴∠ OBC=90°,即BC⊥OB,∴ BC是⊙ O的切线.
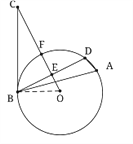
(2)解:∵ OB=6,BC=8,BC⊥OB,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+4x.
(1)写出二次函数y=﹣x2+4x图象的对称轴;
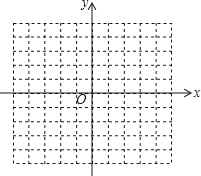
(2)在给定的平面直角坐标系中,画出这个函数的图象(列表、描点、连线);
(3)根据图象,写出当y<0时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
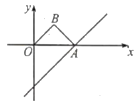
【题目】如图,直线y=x﹣4与x轴交于点A,以OA为斜边在x轴上方作等腰Rt△OAB,并将Rt△AOB沿x轴向右平移,当点B落在直线y=x﹣4上时,Rt△OAB扫过的面积是__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上的 A 、 B 两点所表示的数分别为 a 、b,a b 0 ,ab 0
![]()
(1)原点O 的位置在 ;
A.点 A 的右边 B. 点 B 的左边
C.点 A 与点 B 之间,且靠近点 A D. 点 A 与点 B 之间,且靠近点 B
(2)若 a b 2 ,
①利用数轴比较大小: a 1, b 1 ;(填“>”、“<”或“=”)
②化简:|a-1|+|b+1|.
查看答案和解析>>
科目:初中数学 来源: 题型:
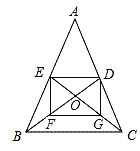
【题目】如图,△ABC的中线BD,CE交于点O,F,G分别是BO,CO的中点.
(1)填空:四边形DEFG是 四边形.
(2)若四边形DEFG是矩形,求证:AB=AC.
(3)若四边形DEFG是边长为2的正方形,试求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )

A. 当AB=BC时,它是菱形 B. 当AC⊥BD时,它是菱形
C. 当∠ABC=90°时,它是矩形 D. 当AC=BD时,它是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠C=90°,AC=BC=2,点D、E分别在边AC、AB上,AD=DE=![]() AB,连接DE.将△ADE绕点A逆时针方向旋转,记旋转角为θ.
AB,连接DE.将△ADE绕点A逆时针方向旋转,记旋转角为θ.
(1)问题发现
①当θ=0°时,![]() = ;
= ;
②当θ=180°时,![]() = .
= .
(2)拓展探究
试判断:当0°≤θ<360°时,![]() 的大小有无变化?请仅就图2的情形给出证明;
的大小有无变化?请仅就图2的情形给出证明;
(3)问题解决
①在旋转过程中,BE的最大值为 ;
②当△ADE旋转至B、D、E三点共线时,线段CD的长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
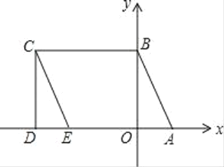
【题目】如图所示,A(1,0)、点B在y轴上,将三角形OAB沿x轴负方向平移,平移后的图形为三角形DEC,且点C的坐标为(-3,2).
(1)直接写出点E的坐标 ;D的坐标
(3)点P是线段CE上一动点,设∠CBP=x°,∠PAD=y°,∠BPA=z°,确定x, y,z之间的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,点M,N分别是AB,CD上两点,点G在AB,CD之间.
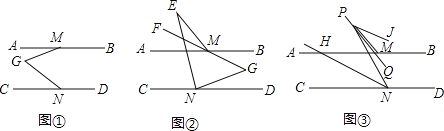
(1)求证:∠AMG+∠CNG=∠MGN;
(2)如图②,点E是AB上方一点,MF平分∠AME,若点G恰好在MF的反向延长线上,且NE平分∠CNG,2∠E+∠G=90°,求∠AME的度数;
(3)如图③,若点P是(2)中的EM上一动点,PQ平分∠MPQ.NH平分∠PNC,交AB于点H,PJ∥NH,直接写出∠JPQ的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com