
【题目】某校要在一块三角形空地上种植花草,如图所示,AC=13 米、AB=14 米、BC=15 米, 若线段 CD 是一条引水渠,且点 D 在边 AB 上.已知水渠的造价每米 150 元.问:点 D 与点 C 距离多远时,水渠的造价最低?最低造价是多少元?

【答案】点D与点C距离12米时,水渠的造价最低,最低造价是1800元.
【解析】
当CD为AB边上的高时,CD最短,从而水渠造价最低.过C作CD⊥AB于D,设AD=xm,则BD=(14-x)m.在Rt△ACD与Rt△BCD中,运用勾股定理得出CD2=AC2-AD2=BC2-BD2即可列出方程,解方程求出CD长再根据水渠的造价每米150元,进而求解即可.
过C作CD⊥AB于D,设AD=xm,

则BD=(14-x)m.
在Rt△ACD中,CD2=AC2-AD2,
在Rt△BCD中,CD2=BC2-BD2,
所以AC2-AD2=BC2-BD2,即132-x2=152-(14-x)2,
解得x=5,
则CD2=132-52,CD=12,
由于水渠的造价每米150元,所以最低造价是150×12=1800元.
答:点D与点C距离12米时,水渠的造价最低,最低造价是1800元.


科目:初中数学 来源: 题型:
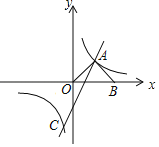
【题目】如图,在平面直角坐标系中,直线y1=2x﹣2与双曲线y2=![]() 交于A、C两点,AB⊥OA交x轴于点B,且OA=AB.
交于A、C两点,AB⊥OA交x轴于点B,且OA=AB.
(1)求双曲线的解析式;
(2)求点C的坐标,并直接写出y1<y2时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算:①13+(﹣22)﹣(﹣2)
②﹣4![]()
③(![]() ×(﹣48)
×(﹣48)
④﹣14﹣(![]() ﹣1)[﹣23+(﹣3)2]
﹣1)[﹣23+(﹣3)2]
(2)化简:①(3mn﹣2m2)+(﹣4m2﹣5mn)
②﹣(2a﹣3b)﹣2(﹣a+4b﹣1)
(3)先化简再求值:7x2y﹣2(2x2y﹣3xy2)-(4x2y﹣xy2),其中x=﹣2,y=1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂为了对新研发的一种产品进行合理定价,将该产品按拟定的价格进行试销,通过对5天的试销情况进行统计,得到如下数据:

(1)通过对上面表格中的数据进行分析,发现销量y(件)与单价![]() (元/件)之间存在一次函数关系,求y关于
(元/件)之间存在一次函数关系,求y关于![]() 的函数关系式(不需要写出函数自变量的取值范围);
的函数关系式(不需要写出函数自变量的取值范围);
(2)预计在今后的销售中,销量与单价仍然存在(2)中的关系,且该产品的成本是20元/件.为使工厂获得最大利润,该产品的单价应定为多少?
(3)为保证产品在实际试销中销售量不得低于30件,且工厂获得得利润不得低于400元,请直接写出单价![]() 的取值范围;
的取值范围;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC 中,AB=15,AC=13,高 AD=12,则△ABC 的周长是( )
A. 42B. 32C. 42 或 32D. 42 或 37
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小梅在餐厅吃饭时,发现了一个有趣的问题:厨师喜欢将做好的油饼都切成一个个小扇形.小梅在想:如果第一次切去圆饼的一半,第二次切去剩余的一半,第三次继续切去剩余的一半,……如图所示.
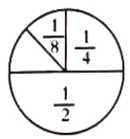
(1)如果继续这样切下去,能把这张油饼切完吗?为什么?
(2)如果依照上面的规律切了10次,那么剩下的油饼是整张油饼的几分之几?
(3)如果厨师照上述方式切了![]() 次,那么他一共将这张油饼切去了多少?
次,那么他一共将这张油饼切去了多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙、丙、丁四位同学给出了四种表示该长方形面积的多项式:
①(2a+b)(m+n);②2a(m+n)+b(m+n);③m(2a+b)+n(2a+b);④2am+2an+bm+bn,你认为其中正确的有( )

A. ①② B. ③④ C. ①②③ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,AB=2,动点D从B开始沿BC向点C运动,到达点C后停止运动,将△ABD绕点A旋转后得到△ACE,则下列说法中,正确的是( )
①DE的最小值为1;②ADCE的面积是不变的;③在整个运动过程中,点E运动的路程为2;④在整个运动过程中,△ADE的周长先变小后变大.

A. ①③④ B. ①②③ C. ②③④ D. ①②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com